Introducción al análisis de la dinámica de sistemas

Ejemplos prácticos

Péndulo simple

Considere el péndulo simple mostrado en la siguiente figura

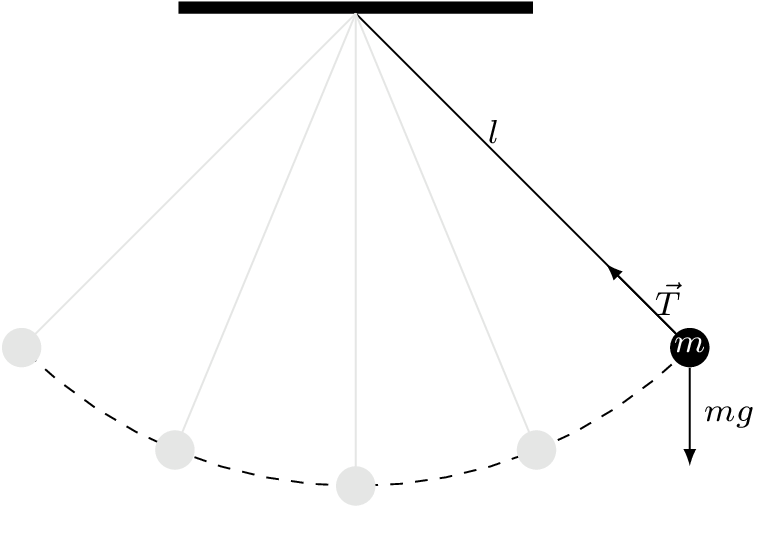
Fig. 1 Diagrama de péndulo simple sin fuerza externa.

donde \(l\) denota la longitud de la barra, y \(m\) la masa de la bola. Asuma que la barra es rígida y de masa despreciable. Suponga entonces, \(\theta\) como el ángulo entre la barra y el eje vertical a través del pivote. Además, el péndulo se mueve libremente sobre un plano vertical formando un círculo de radio \(l\). Para obtener la ecuación que describe el movimiento del péndulo es necesario identificar las fuerzas que interactúan sobre la bola o bien, utilizar el enfoque de Euler-Lagrange.

Modelado a partir de leyes físicas

En un sistema mecánico de tipo rotacional, las leyes físicas que rigen el sistema están dadas por la Segunda ley de Newton, donde las fuerzas positivas están dadas hacia la derecha mientras que las negativas hacia el lado contrario. Si realizamos un diagrama de cuerpo libre para observar las fuerzas que interactúan con la masa como se muestra a continuación

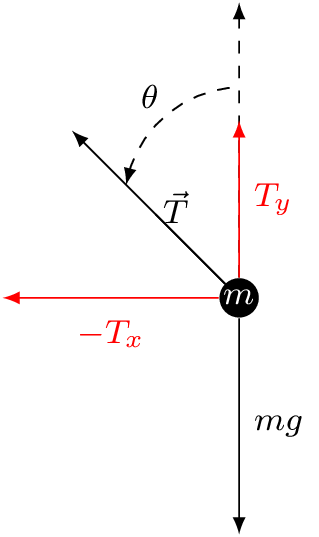
Fig. 2 Diagrama de cuerpo libre de la masa en el péndulo simple.

Podemos observar que hay una fuerza gravitacional \(mg\), donde \(g\) es la aceleración de la gravedad. Así mismo, existe una fuerza de tensión \(\vec{T}\) con componentes \(T_{x}\) y \(T_{y}\).

Podemos observar que la única fuerza que interactúa en \(x\) es \(T_{x}\). Recordando que esta tensión tiene una fuerza negativa, por lo tanto la definimos como sigue

(1)\[ -T\sin(\theta) = m \ddot{x}, \]

donde \(T\) denota la magnitud de la tensión y \(\ddot{x}:=\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\).

Para el análisis de las fuerzas que interactúan en el eje \(y\), tenemos

(2)\[ -mg + T\cos(\theta) = m\ddot{y}. \]

Observamos entonces que tenemos mas variables que ecuaciones. Por ello, vamos a relizar el siguiente despeje

(3)\[ T = -\frac{m \ddot{x}}{\sin(\theta)}. \]

Sustituyendo (3) en (2), tenemos

(4)\[ -mg + \left(-\frac{m\ddot{x}}{\sin(\theta)}\right)\cos(\theta) = m \ddot{y}. \]

Simplificamos la expresión obtenida multiplicando ambos lados de la igualdad por el término \(\sin(\theta)\) y resulta

(5)\[ -mg\sin(\theta) - m\ddot{x}\cos(\theta) = m \ddot{y}\sin(\theta). \]

Observando el diagrama de la Fig. 1, tenemos que la posición de la masa está dada por sus componentes \(x\) e \(y\) dentro de un plano cartesiano. Así mismo, tenemos que \(l\) y \(\theta\) están en un sistema de coordenadas polares. Por lo tanto, podemos utilizar la relación que hay entre estos sistemas para establecer las siguientes relaciones

(6)\[ x = l\sin(\theta), \quad y = -l\cos(\theta). \]

Puesto que necesitamos la aceleración a lo largo del eje \(x\) e \(y\), derivamos la expresión dada en la (6) recordando la regla de la cadena

(7)\[\begin{split} \begin{aligned} \dot{x} &= l\cos(\theta)\dot{\theta}, \\ \dot{y} &= l\sin(\theta)\dot{\theta}, \\ \end{aligned} \end{split}\]

(8)\[\begin{split} \begin{aligned} \ddot{x} &= l \left[\ddot{\theta}\cos(\theta) - \dot{\theta}^{2}\sin(\theta) \right],\\ \ddot{y} &= l \left[\ddot{\theta}\sin(\theta) + \dot{\theta}^{2}\cos(\theta) \right]. \\ \end{aligned} \end{split}\]

Sustituyendo (7) y (8) en (5)

(9)\[\begin{split} \begin{aligned} -mg\sin(\theta) - ml\ddot{\theta}\cos^{2}(\theta) + ml\dot{\theta}^{2}\sin(\theta) \cos(\theta) &= ml \ddot{\theta}\sin^{2}(\theta) + ml\dot{\theta}^{2}\cos(\theta) \sin(\theta), \\ -mg\sin(\theta) - ml\ddot{\theta}\cos^{2}(\theta) &= ml \ddot{\theta}\sin^{2}(\theta), \\ -mg\sin(\theta) &= ml\ddot{\theta} \left[\sin^{2}(\theta) + \cos^{2}(\theta)\right], \\ \end{aligned} \end{split}\]

(10)\[ ml\ddot{\theta} = -mg\sin(\theta). \]

Suponiendo que hay una fuerza proporcional a la velocidad de la masa con un coeficiente \(k_{f}\) que resiste el movimiento, el modelo de péndulo simple con fuerza de fricción queda dado por la siguiente ecuación

(11)\[ ml\ddot{\theta} = -mg\sin(\theta) - k_{f}l\dot{\theta}. \]

Por lo tanto, la dinámica del péndulo simple con y sin fricción están dadas por ecuaciones diferenciales de segundo orden. Para resolver las Ecs. (10) y (11) realizamos un cambio de variable y definimos como variables de estado \(x_{1} = \theta\) y \(x_{1} = \dot{\theta}\). Por consiguiente, el sistema queda representado como sigue

(12)\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= -\frac{g}{l} \sin(x_{1}) - \frac{k_{f}}{m}x_{2}. \end{aligned} \end{split}\]

Una variante del sistema de péndulo simple se puede obtener agregando una entrada exógena \(\tau\)

\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= -\frac{g}{l} \sin(x_{1}) - \frac{k_{f}}{m}x_{2} + \frac{\tau}{ml^{2}}. \end{aligned} \end{split}\]

Modelado a partir del enfoque Euler-Lagrange

Cualquier sistema debe satisfacer las ecuaciones de Lagrange dadas por

(13)\[ \frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{\partial \mathcal{L}}{\partial\dot{q}} \right] - \frac{\partial \mathcal{L}}{\partial q} + \frac{\partial J}{\partial \dot{q}} = 0, \]

donde \(\mathcal{L}\) es el Lagrangiano del sistema y se define como sigue

\[ \mathcal{L}(q,\dot{q}) = U^{*}(\dot{q})-T(q). \]

Además

• \(U\), representa la coenergía total en las reservas de flujo del sistema expresada como una función de las coordenadas de esfuerzo generalizado.

• \(T\), la energía total en los almacenes de esfuerzo del sistema expresada como una función de las coordenadas de acumulación de esfuerzo generalizadas.

• \(J\), el co-contenido total en los disipadores del sistema expresado como una función de las coordenadas de esfuerzo generalizado.

• \(q\), el vector de coordenadas generalizadas definida como el conjunto de coordenadas linealmente independientes que definen la configuración del sistema.

Para un sistema mecánico no conservativo, las ecuaciones de Lagrange están dadas como sigue

(14)\[ \frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{\partial \mathcal{L}}{\partial\dot{q}_{j}} \right] - \frac{\partial \mathcal{L}}{\partial q_{j}} + \frac{\partial J}{\partial \dot{q}_{j}} = \tau_{j}, \quad j = 1,\dots,l. \]

donde \(\tau_{j}\) denota las fuerzas generalizadas.

Hint

En este contexto conservativo significa libre de disipación y entradas de fuerzas externas.

El sistema mostrado en la Fig. 1, sólo posee un grado de libertad denotado como \(\theta\). Entonces, definimos las siguientes coordenadas generalizadas

\[ q := \theta, \quad \dot{q} := \dot{\theta}. \]

Además, definimos como fuerza generalizada la variable \(u\), i.e.

\[ \tau_{i} = 0. \]

Ahora bien, podemos representar la Ec. (6) en forma vectorial como sigue

(15)\[\begin{split} p_{m} = \begin{bmatrix} x_{m} \\ y_{m} \end{bmatrix} = \begin{bmatrix} l\sin(\theta) \\ -l\cos(\theta) \end{bmatrix}, \end{split}\]

y el vector de velocidad (7) como sigue

(16)\[\begin{split} v_{m} = \begin{bmatrix} \dot{x}_{m} \\ \dot{y}_{m} \\ \end{bmatrix} = \begin{bmatrix} l\cos(\theta)\dot{\theta} \\ l\sin(\theta)\dot{\theta} \\ \end{bmatrix}. \end{split}\]

La energía co-cinética del sistema está dada por

(17)\[\begin{split} \begin{aligned} U^{*} = \frac{1}{2}mv^{2} &\equiv \frac{1}{2}m\|v_{m}\|^{2}\\ &= \frac{1}{2}mv_{m}^{T}v_{m}. \end{aligned} \end{split}\]

mientras que la energía potencial del sistema por

(18)\[ T = mgh \equiv m\vec{g}^{T}p_{m}, \]

donde \(\vec{g} = \begin{bmatrix} 0 & g \end{bmatrix}^{T}\), con \(g \in \mathbb{R}^{2}\).

Sustituyendo (16) en (17), tenemos

\[\begin{split} \begin{aligned} U^{*} &= \frac{1}{2}m \begin{bmatrix} l\cos(\theta)\dot{\theta} & l\sin(\theta)\dot{\theta} \end{bmatrix} \begin{bmatrix} l\cos(\theta)\dot{\theta} \\ l\sin(\theta)\dot{\theta} \\ \end{bmatrix} \\ &= \frac{1}{2}m \left( l^{2}\cos^{2}(\theta)\dot{\theta}^{2} + l^{2}\sin^{2}(\theta)\dot{\theta}^{2} \right), \\ &= \frac{1}{2} ml^{2}\dot{\theta}^{2} \left( \cos^{2}(\theta) + \sin^{2}(\theta) \right), \\ &= \frac{1}{2} ml^{2}\dot{\theta}^{2}. \end{aligned} \end{split}\]

Ahora, sustituyendo (15) en (18)

\[\begin{split} \begin{aligned} T &= m \begin{bmatrix} 0 & g \end{bmatrix} \begin{bmatrix} l\sin(\theta) \\ -l\cos(\theta) \end{bmatrix}, \\ &= -mgl\cos(\theta) \end{aligned} \end{split}\]

Entonces, el Lagrangiano del sistema se define como sigue

\[ \mathcal{L} = \frac{1}{2}ml^{2}\dot{\theta}^{2} + mgl\cos(\theta). \]

Obtenemos las derivadas parciales

(19)\[ \frac{\partial \mathcal{L}}{\partial \dot{\theta}} = ml^{2}\dot{\theta}, \]

(20)\[ \frac{\mathrm{d}}{\mathrm{d}t}\left[ \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right]= ml^{2}\ddot{\theta}, \]

(21)\[\begin{split} \begin{aligned} \frac{\partial \mathcal{L}}{\partial \theta} &= \frac{\partial}{\partial \theta} \left( \frac{1}{2}ml^{2}\dot{\theta}^{2} + mgl\cos(\theta) \right), \\ &= -mgl\sin(\theta), \end{aligned} \end{split}\]

Sustituyendo, (19)-(21) en (14) y considerando que \(\tau=0\) tenemos

\[ ml^{2}\ddot{\theta} + mgl\sin(\theta) = 0. \]

Diodo tunel

El circuito de diodo tunel se muestra en la siguiente figura

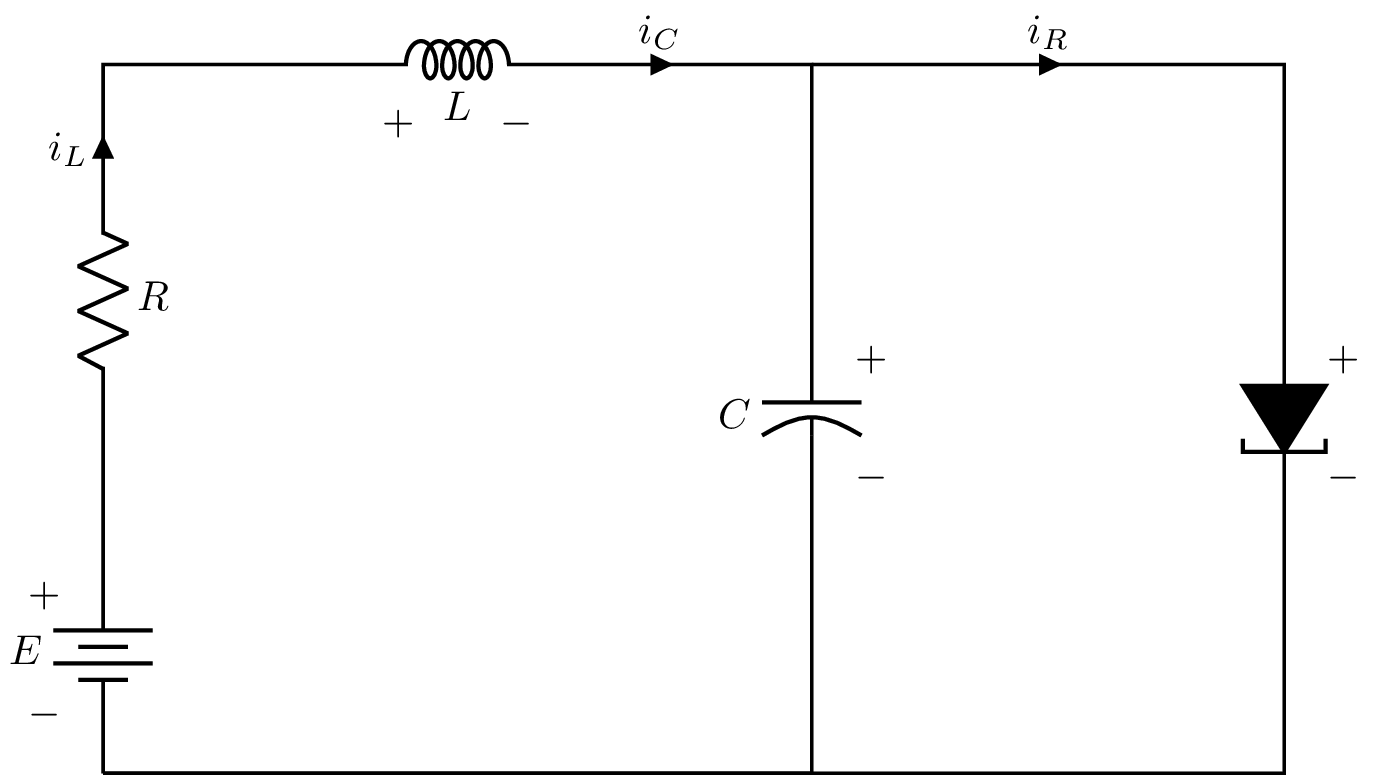
Fig. 3 Diodo túnel.

donde la relación constitutiva que caracteriza el tunel diodo está dada por \(i_{R} = h(v_{R})\). Los elementos almacenadores de energía son el inductor \(L\) y el capacitor \(C\). Asumiendo que estos elementos son lineales e invariantes en el tiempo, podemos llegar a representar este sistema a partir del siguiente modelo

(22)\[\begin{split} \begin{aligned} i_{C} &= C \dot{v}_{C}, \\ v_{L} &= L \frac{\mathrm{d}i_{L}}{\mathrm{d}t}, \end{aligned} \end{split}\]

donde \(v\) e \(i\) denotan el voltaje y corriente a través de un elemento. Además, el sub índice especifica el elemento.

Las ecuaciones del circuito de diodo tunel se pueden representar en forma de espacio-estados si consideramos \(u=E\) como una entrada constante, \(x_{1} = v_{C}\) (tensión en el capacitor) y \(x_{2} = i_{L}\) (corriente en el inductor).

Utilizando las Leyes de Kirchhoff y expresando \(i_{C}\) como una función de las variables de estado \(x_{1}\), \(x_{2}\) y la entrada \(u\), tenemos lo siguiente

\[ i_{C} + i_{R} - i_{L} = 0, \]

por consiguiente

\[ i_{C} = -h(x_{1}) + x_{2}. \]

Del mismo modo, expresamos \(v_{L}\) como una función de las variables \(x_{1}\), \(x_{2}\), \(u\) y utilizamos las Leyes de Kirchhoff como sigue

\[ v_{C} - E + Ri_{L} + v_{L} = 0. \]

donde \(v_{L} = -x_{1} - Rx_{2} + u\).

Reescribiendo las ecuaciones del sistema (22), tenemos

(23)\[\begin{split} \begin{aligned} \dot{x}_{1} &= \frac{1}{C}\left(-h(x_{1}) + x_{2} \right) ,\\ \dot{x}_{2} &= \frac{1}{L}\left(-x_{1} - Rx_{2} + u \right), \end{aligned} \end{split}\]

Circuito R-C

La relación que establece el flujo electromagnético \(\phi\) y la corriente \(i\) que lo produce está dada por la siguiente ecuación

\[ \phi = L i, \]

donde \(L\) es una constante que depende de los factores geométricos y de entorno llamada inductancia.

Los cambios de flujo electromagnético originan potenciales eléctricos relacionados por la Ley de Faraday

\[ u_{L} = - \dot{\phi}, \]

donde \(u_{L}\) denota el voltaje en las terminales de la inductancia a razón del cambio de flujo. Por consiguiente, la Ley de Faraday se puede expresar como sigue

\[ u_{L} = - L \dot{\phi}. \]

En elementos resistivos el voltaje \(u_{R}\) entre el componente y la corriente \(i\) que circula por él obedecen a la Ley de Ohm dada como siguiente

(24)\[ u_{R} = Ri, \]

donde \(R\) es una constante que depende del componente denominado resistencia.

El voltaje \(u_{C}\) entre las terminales de una capacitancia y la carga \(q\) siguen la siguiente relación

\[ u_{C} = \frac{Q}{C} \equiv \frac{1}{C} \int i \mathrm{d}t, \]

donde \(C\) es una constante que depende de la geometría y el entorno denominada capacitancia. Si consideramos que la corriente se define como una variación temporal de carga

\[ i = \dot{Q}, \quad Q = \int i \mathrm{d}t, \]

entonces \(u_{C}\) se expresa en los siguientes términos

(25)\[ u_{C} = \frac{1}{C} \int i\mathrm{d}t. \]

Considere el circuito mostrado en la Fig. 4

Aplicando la Ley de tensiones de Kirchhoff, obtenemos

(26)\[ u_{R} + u_{C} = V_{in}. \]

Sustituyendo (24) y (25) en (26), tenemos

\[ Ri + \frac{1}{C} \int i \mathrm{d}t = V_{in}, \]

expresado la ecuación anterior en términos de la carga \(Q\), tenemos la siguiente expresión

(27)\[ R \dot{Q} + \frac{1}{C}Q = V_{in}, \]

Aplicando la Ley de corrientes de Kirchhoff, obtenemos

\[ i_{R} + i_{C} = i, \]

dado que el voltaje entre los componentes eléctricos es el mismo y lo denotamos por \(u\), tenemos

\[ \frac{u}{R} + C \dot{u} = i. \]

Considerando el modelo dado en la Ec. (27) y tomando \(V\) como la carga en el capacitor dividida por la capacitancia \(V := \frac{Q}{C}\) y \(\dot{V}:= \frac{\dot{Q}}{C}\), sustituyendo tenemos

\[\begin{split} \begin{aligned} R\dot{V}C + \frac{1}{C}VC &= V_{in}, \\ R\dot{V}C + V &= V_{in}. \end{aligned} \end{split}\]

Entonces, el modelo del circuito RC mostrado en la Fig. 4 está dado por la siguiente ecuación

\[ \dot{V} + \frac{1}{RC}V = \frac{1}{RC} V_{in}. \]

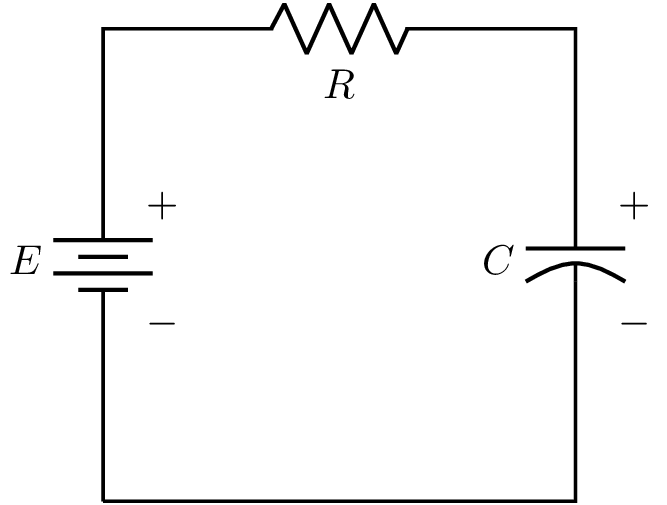
Fig. 4 Modelo de circuito R-C.

Sistema masa-resorte

Considere una masa \(m\) que se desliza sobre una superficie horizontal y que se encuentra sujeta a una superficie vertical a través de un resorte con constante de fuerza \(k\) como se muestra en la siguiente figura.

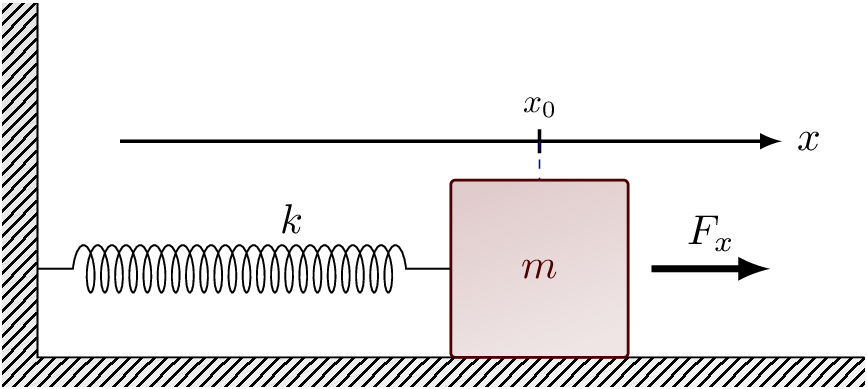
Fig. 5 Diagrama del sistema masa-resorte.

Si definimos \(x\) como el desplazamiento desde el punto de referencia \(x_{0}\); asumimos que la masa se desplaza sin fricción y aplicamos la Segunda ley de Newton así como la Ley de Hooke obtenemos

(28)\[ ma + kx = F_{x}. \]

Dado que la aceleración \(a\) está definida como \(\ddot{x}\) y que la fuerza \(F_{x}\) está a nuestra disposición, sustituimos en la ecuación anterior para obtener el modelo del sistema masa-resorte como sigue

\[ m\ddot{x} + kx = 0. \]

Para un desplazamiento largo, la fuerza restauradora (\(kx\)) podría depender de manera no lineal de \(x\), por ejemplo, expresada por la siguiente función

\[ g(x) = k\left( 1 - a^{2}x^{2} \right)x, \quad |ax|<1, \]

representa al modelo llamado softening spring, donde un gran incremento de desplazamiento produce un incremento pequeño de fuerza.

Por otro lado, si tenemos la siguiente función

\[ g(x) = k\left(1 + a^{2}y^{2} \right)x, \]

es posible obtener el modelo llamado hardening spring donde un incremento pequeño de desplazamiento produce un gran incremento de fuerza.

Modelado a partir del enfoque Euler-Lagrange

En este caso, vamos a tratar de obtener el modelo dinámico del sistema masa-resorte utilizando las ecuaciones de Euler-Lagrange. Para ello, definimos la siguiente coordenada generalizada

\[ q = x, \quad \dot{q} = \dot{x}. \]

Expresamos las energías en función de la coordenada generalizada para obtener el Lagrangiano del sistema. Donde, la energía potencial del sistema se obtiene a partir de la siguiente relación

(29)\[ A = \frac{\text{base}\cdot \text{altura}}{2}, \]

Sustituyendo la Ley de Hooke en (29), tenemos

\[ T = \frac{qkq}{2} \equiv \frac{kq^{2}}{2}, \]

mientras que la co-energía cinética está dada como sigue

\[ U^{*} = \frac{m\dot{q}^{2}}{2}. \]

Por consiguiente, el Lagrangiano del sistema se define como sigue

(30)\[ \mathcal{L}(q,\dot{q}) = \frac{m\dot{q}^{2}}{2} - \frac{kq^{2}}{2}. \]

Calculando las ecuaciones de Lagrange (14) a partir de la ecuación (30), obtenemos

\[ \frac{\partial \mathcal{L}}{\partial \dot{q}} = m\dot{q} \]

(31)\[ \frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac{\partial \mathcal{L}}{\partial \dot{q}} \right] = m\ddot{q} \]

(32)\[ \frac{\partial \mathcal{L}}{\partial q} = -kq \]

Finalmente, sustituimos las Ecs. (31), (32) en la Ec. (14)

\[ m\ddot{x} + kx = F_{x}. \]

Sistema masa-resorte-amortiguador

Considere el sistema masa-resorte-amortiguador mostrado en la siguiente Figura.

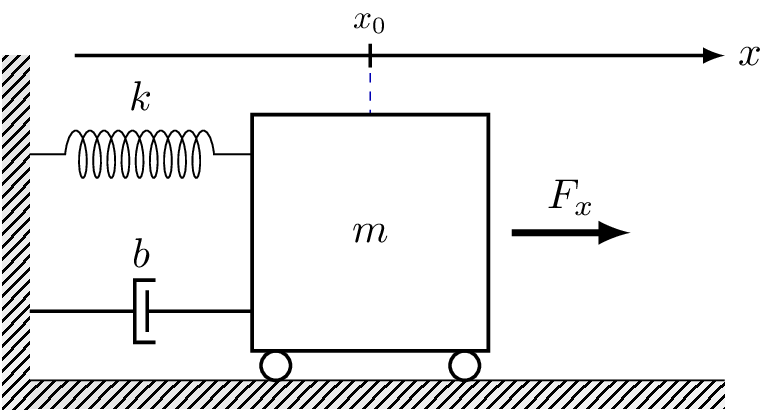
Fig. 6 Sistema masa-resorte-amortiguador.

Dicho sistema consiste en una masa \(m\) sujeta a un elemento de amortiguamiento con constante de viscosidad \(b\) y un resorte con rigidez \(k\). Podemos observar que el sistema se desplaza sobre un plano horizontal a partir de una fuerza \(F_{x}\) aplicada.

Podemos partir del modelo dado en la Ec. (28) y modelando el amortiguador con la relación dada a continuación

\[ F_{k} = b \dot{x}, \]

donde \(b\) denota el coeficiente de fricción viscosa, tenemos

\[ m\ddot{x} + b\dot{x} + kx = F_{x}. \]

De manera análoga, podemos obtener aplicar las ecuaciones de Lagrange (14) considerando que existe una fuerza de fricción viscosa como sigue

\[ m\ddot{x} + kx = F_{x} - b\dot{x}. \]

Índices de error

Criterios integrales

Integral del error absoluto (IAE)

\[ \text{IAE} = \int_{0}^{\infty} | e(t) |\mathrm{d} t, \]

donde

\[ e(t) = y(t) - \hat{y}(t). \]

• Fácil aplicación

• No se pueden optimizar sistemas altamente sub ni altamente sobre amortiguados

• Difícil de evaluar analíticamente

def IAE(y,yg,dt):
    return np.trapz(np.abs(y-yg))*dt

Integral del tiempo por el error absoluto (ITAE)

• Los errores tardíos son más castigados

• Buena selectividad

• Difícil de evaluar analíticamente

def ITAE(y,yg,t,dt):
    return np.trapz(t*np.abs(y-yg))*dt

Integral del error cuadrático (ISE)

\[ \text{ISE} = \int_{0}^{\infty} e^{2}(t)\mathrm{d}t. \]

• Da mayor importancia a los errores grandes

• No es un criterio muy selectivo

• Respuesta rápida pero oscilatoria, estabilidad pobre

def ISE(y,yg,dt):
    return np.trapz(np.abs(y-yg)**2)*dt

Integral del tiempo por el error cuadrático (ITSE)

\[ \text{ITSE} = \int_{0}^{\infty} te^{2}(t)\mathrm{d}t. \]

• Los grandes errores iniciales tienen poco peso pero los que se producen más tarde son fuertemente penados

• Mejor selectividad con respecto al ISE

def ITSE(y,yg,t,dt):
    return np.trapz(t*(y-yg)**2)*dt

Criterios estadísticos

Mean Square Error

\[ \text{MSE} = \frac{1}{N} \sum_{k=0}^{N} e_{k}^{2}. \]

• No recomendable para estudiar modelos de predicción

• No tiene escala original el error porque está elevado al cuadrado

• No se mide en unidades de los datos experimentales

def MSE(y,yg):
    e = y - yg
    return np.mean(e**2)

Root Mean Square Error

\[ \text{RMSE} = \sqrt{\frac{1}{N} \sum_{k=0}^{N} e_{k}^{2}}. \]

• Sensible a valores atípicos

• No se ajusta a la demanda (¿qué es demanda?)

• Se mide en unidades de los datos experimentales

def RMSE(y,yg):
   return np.sqrt(MSE(y,yg))

Mean Absolute Error

\[ \text{MAE} = \frac{1}{N} \sum_{k=0}^{N} |e_{k}|. \]

• Mide la precisión de los datos simulados

• Se mide en unidades de los datos experimentales

• No es sensible a valores atípicos

• Utilizado para analizar series temporales

def MAE(y,yg):
   return np.mean(np.abs(y-yg))

Mean Absolute Percentage Error

\[ \text{MAPE} = \frac{100\%}{N} \sum_{k=0}^{N} \left| \frac{e_{k}}{y_{k}} \right| \]

• Mide el error en porcentajes

• Indicador de desempeño

• Fácil interpretación

• Ampliamente utilizado para evaluar modelos de predicción

Tabla de MAPE

• Si \(\text{MAPE}<10\), entonces el modelo es altamente preciso

• Si \(10<\text{MAPE}<20\), entonces el modelo es bueno

• Si \(20<\text{MAPE}<50\), entonces el modelo es razonable

• Si \(\text{MAPE}>50\), entonces el modelo es impreciso

FIT

Obtiene el porcentaje de variación de salida que es explicado por un modelo

\[ \text{FIT} = 100\left(1 - \frac{\|y - \hat{y}\|}{\|y - \bar{y}\|}\right) \]

---

Métodos numéricos

Método de Euler

Sea \(\phi(x)\) la solución exacta de la ecuación diferencial

\[ \dot{y}(x) = f(x,y), \]

con condición iniciales

\[ y(x_{0}) = y_{0}, \]

donde \(\phi(x)\) satisface la relación

\[ \dot{\phi}(x) = f(x,\phi(x)),\quad \phi(x_{0}) = y_{0}. \]

La solución de una ecuación diferencial vía numérica es una solución aproximada del valor de la solución \(\phi(x)\) en un conjunto finito de puntos. Es decir, \(\phi(x_{n}):y_{n}\approx \phi(x_{n})\).

Es común elegir los puntos \(x_{n}\) de forma equiespaciada, esto es \(h = x_{n+1} - x_{n}\). En este caso, \(x_{n} = x_{0} + nh\) donde \(h\) es el tamaño del paso.

Integramos la relación dada en la ecuación anterior entre \(x_{0}\) y \(x_{1}\)

\[ \int_{x_{0}}^{x_{1}} f(x,\phi(x))~ \mathrm{d}x = \int_{x_{0}}^{x_{1}} \dot{\phi}(x)~\mathrm{d}x = \phi(x_{1}) - \phi(x_{0}), \]

o bien

\[ \phi(x_{1}) = \phi(x_{0}) + \int_{x_{0}}^{x_{1}} f(x,\phi(x))~ \mathrm{d}x. \]

Recordando que \(\phi(x_{0}) = y_{0}\), entonces

\[ \phi(x_{1}) = y_{0} + \int_{x_{0}}^{x_{1}} f(x,\phi(x))~\mathrm{d}x, \]

podemos hallar el valor de \(\phi(x_{1})\) evaluando la integral anterior.

El método de Euler estima esta integral mediante la regla del rectángulo

\[ \int_{x_{0}}^{x_{1}} f(x,\phi(x))~\mathrm{d}x \approx f(x_{0},y_{0})(x_{1}-x_{0}). \]

Es decir, aproxima el área que hay bajo la curva \(f(x,\phi(x))\) entre \(x_{1}\) y \(x_{0}\) por el área del rectángulo de ancho \((x_{1}-x_{0})\) con altura igual a la ordenada de la curva en su extremo izquierdo \(f(x_{0},y_{0})\)

\[ \phi(x_{1}) \approx \phi(x_{0}) + f(x_{0},\phi(x_{0}))h. \]

Para estimar el valor de \(\phi(x)\) en el siguiente punto \(x_{2}\), integramos entre \(x_{1}\) y \(x_{2}\), i.e.

\[ \int_{x_{1}}^{x_{2}} \dot{\phi}(x)~\mathrm{d}x = \phi(x_{2}) - \phi(x_{1}) = \int_{x_{1}}^{x_{2}} f(x, \phi(x))~\mathrm{d}x. \]

Aproximando la integral mediante la regla del rectángulo se tiene

\[ \phi(x_{2}) \approx \phi(x_{1}) + f(x_{1},\phi(x_{1}))(x_{2}-x_{1}). \]

Dado que \(\phi(x_{1})\) es desconocido, entonces lo aproximamos por \(y_{1}\) como sigue

\[\begin{split} \begin{aligned} \phi(x_{2}) & \approx \phi(x_{1}) + f(x_{1},\phi(x_{1}))(x_{2}-x_{1}), \\ \phi(x_{2}) & \approx y_{1} + f(x_{1},y_{1})(x_{2}-x_{1}), \end{aligned} \end{split}\]

o bien

\[ \phi(x_{2}) \approx y_{1} + f(x_{1},y_{1})h. \]

Estimando \(\phi(x_{2})\) por \(y_{2}\), entonces cualquier estimación \(y_{n+1}\) de \(\phi(x_{n+1})\) puede hacerse por el método de Euler de acuerdo con la siguiente expresión

\[ \phi(x_{n+1}) \approx y_{n+1} = y_{n} + f(x_{n},y_{n})h \]

Método de Runge-Kutta

Sirve para buscar aproximaciones a la solución en puntos intermedios del intervalo \([x_{n},x_{n+1}]\) con una combinación lineal de los valores de la derivada en varias aproximaciones para obtener un valor de \(y_{n+1}\).

Sea la ecuación diferencial

\[ \dot{y}(x) = f(x,y), \quad y(y_{0}) = y_{0}, \]

y sea

\[ x_{n} = x_{0} + nh, \quad h>0. \]

Para evaluar \(y(x_{n+1})\) conociendo el valor \(y_{n}\) y además \(0 \leq \alpha_{1} \leq \alpha_{2} \cdots \leq \alpha_{r} \leq 1\), de modo que \(\sum_{n=1}^{r}\gamma_{n} = 1\), el método de Runge-Kutta evalúa \(y_{n+1}\) como sigue

\[ y_{n+1} = y_{n} + \sum_{n=1}^{r} \gamma_{n}k_{n}, \]

donde

\[ k_{n} = h~f\left(x_{n} + \alpha_{n}h, y_{n} + \sum_{j=1}^{r}\beta_{n,j}k_{j}\right), \quad \sum_{j=1}^{r} \beta_{n,j} = \alpha_{n}. \]

Los métodos de Runge-Kutta se clasifican en:

• Explícitos. Cuando los valores de \(k_{n}\) pueden ser evaluados en función de \(k_{1},k_{2},\dots,k_{n-1}\).

• Implícitos. Cuando lo anterior no es posible.

Además, en los métodos explícitos se satisface la siguiente restricción

\[ \beta_{n,j} = 0, ~ \forall n \leq j. \]

Mientras que para los implícitos se resuelve en cada paso un sistema de ecuaciones de la forma

\[\begin{split} \begin{aligned} k_{1} &= f\left( x_{n} + \alpha_{1}h, y_{n} + \beta_{1,1}k_{1} + \beta_{1,2}k_{2} + \cdots + \beta_{1,p}k_{p} \right), \\ k_{2} &= f\left( x_{n} + \alpha_{2}h, y_{n} + \beta_{2,1}k_{1} + \beta_{2,2}k_{2} + \cdots + \beta_{2,p}k_{p} \right), \\ \vdots ~ &= ~ \vdots \\ k_{p} &= f\left( x_{n} + \alpha_{p}h, y_{n} + \beta_{p,1}k_{1} + \beta_{p,2}k_{2} + \cdots + \beta_{p,p}k_{p} \right). \end{aligned} \end{split}\]

El méto de Runge-Kutta de 4to orden es el más utilizado y evalúa la función \(f(x,y)\) en los puntos \(x_{n}\), \(x_{n}+\frac{h}{2}\) y \(x_{n} + h\) de la forma

\[ y_{n+1} = y_{n} + \alpha_{1}k_{1} + \alpha_{2}k_{2} + \alpha_{3}k_{3} + \alpha_{4}k_4, \]

con

\[\begin{split} \begin{aligned} k_{1} &= f\left(x_{n},y_{n} \right)h, \\ k_{2} &= f\left(x_{n} + a_{2}h,y_{n} + b_{21}k_{1} \right)h, \\ k_{3} &= f\left(x_{n} + a_{3}h,y_{n} + b_{31}k_{1} + b_{32}k_{2} \right)h, \\ k_{4} &= f\left(x_{n} + a_{4}h,y_{n} + b_{41}k_{1} + b_{42}k_{2} + b_{43}k_{3} \right)h. \end{aligned} \end{split}\]

Eligiendo arbitrariamente \(\alpha_{2}=\alpha_{3}=\frac{1}{3}\) y hallando el resto de los coeficientes mediante un sistema algebráico de 11 ecuaciones, tenemos

\[\begin{split} \begin{aligned} \alpha_{1} &= \frac{1}{6}, \\ \alpha_{2} &= \frac{1}{3},~ \alpha_{2} = \frac{1}{2},~ b_{21} = \frac{1}{2}, \\ \alpha_{3} &= \frac{1}{3}, ~ \alpha_{3} = \frac{1}{2}, ~ b_{31} = 0, ~ b_{32} = \frac{1}{2}, \\ \alpha_{4} &= \frac{1}{6}, ~ \alpha_{4} = 1, ~ b_{41} = 0, ~ b_{42} = 0, ~ b_{43} = 1. \end{aligned} \end{split}\]

Tendríamos entonces

\[ y_{n+1} = y_{n} + \frac{1}{6}\left(k_{1} + 2k_{2} + 2k_{3} + k_{4} \right), \]

con

\[\begin{split} \begin{aligned} k_{1} &= f\left( x_{n},y_{n} \right)h, \\ k_{2} &= f\left( x_{n} + \frac{h}{2},y_{n} + \frac{k_{1}}{2} \right)h, \\ k_{3} &= f\left( x_{n} + \frac{h}{2},y_{n} + \frac{k_{2}}{2} \right)h, \\ k_{4} &= f\left( x_{n} + h,y_{n} + k_{3}\right)h. \end{aligned} \end{split}\]