Fundamentos del análisis de estabilidad en el sentido de Lyapunov

Considere un sistema autónomo representado por la siguiente ecuación

(35)\[ \dot{x} = f(x), \]

donde \(f:D\leftarrow R^{n}\) es un mapa local de Lipschitz de un dominio \(D\subset R^{n}\) en \(R^{n}\).

Para poder estudiar la estabilidad del sistema (35), es necesario obtener \(\bar{x}\in D\) que denota el punto de equilibrio

\[ f(\bar{x}) = 0. \]

Localización de los puntos de equilibrio

Definition 1

El punto de equilibrio \(x=0\) de \(\dot{x} = f(x)\) es

estable si, para cada \(\varepsilon >0\), hay un \(\delta = \delta(\varepsilon)>0\) tal que

\[ \|x(0)\| < \delta \Rightarrow \|x(t)\| < \varepsilon, \quad \forall t\geq 0 \]

• inestable si no es estable.

• asintóticamente estable si este es estable y \(\delta\) se escoge tal que.

\[ \|x(0)\| < \delta \Rightarrow \lim \limits_{t\rightarrow \infty} x(t) = 0. \]

Ejemplo 1.

Considere las ecuaciones del péndulo simple y obtenga sus puntos de equilibrio

\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= - \frac{g}{l}\sin(x_{1}) - \frac{k}{m}x_{2}. \end{aligned} \end{split}\]

---

Linealización de sistemas en torno a un punto de equilibrio

Un sistema (LTI) de la forma

(36)\[ \dot{x} = Ax, \]

tiene un punto de equilibrio en el origen. Este punto de equilibrio está aislado si y sólo si \(\text{det}(A)\neq0\). Si \(\text{det}(A)=0\), la matriz \(A\) tiene un espacio nulo no trivial.

Las propiedades de estabilidad del origen pueden ser caracterizadas por las ubicaciones de los eigenvalores de la matriz \(A\).

Recordemos que la solución al sistema \(\dot{x}=Ax\) dada una condición inicial \(x_{0}\) está dada como sigue

\[ x(t) = \exp(At)x_{0}. \]

Además, para cualquier matriz \(A\) existe una matriz \(P\) no \myindex{singular} que transforma \(A\) en su forma de Jordan, i.e.

\[ P^{-1}AP = J = \text{block} \text{diag}\left[J_{1}, J_{2},\dots, J_{r} \right], \]

donde \(J_{i}\) es el bloque de Jordan asociado con el eigenvalor \(\lambda_{i}\) de A.

La forma generalizada del bloque de Jordan, considerando un orden \(m\), tiene la forma siguiente

\[\begin{split} J_{i} = \begin{bmatrix} \lambda_{i} & 1 & 0 & \cdots & \cdots & 0 \\ 0 & \lambda_{i} & 1 & 0 & \cdots & 0 \\ \vdots & & \ddots & & & \vdots \\ \vdots & & & \ddots & & 0 \\ \vdots & & & & \ddots & 1 \\ 0 & \cdots & \cdots & \cdots & 0 & \lambda_{i} \end{bmatrix}_{m\times m}, \end{split}\]

por consiguiente

\[ \exp(At) = P \exp(Jt)P^{-1} = \sum_{i=1}^{r} \sum_{k=1}^{m_{i}} t^{k-1} \exp(\lambda_{i}t) R_{ik}, \]

donde \(m_{i}\) es el orden del bloque de Jordan asociado con el eigenvalor \(\lambda_{i}\).

Theorem 6

El punto de equilibrio \(x=0\) de \(\dot{x} = Ax\) es estable si y sólo si todos los eigenvalores de \(A\) satisfacen \(\text{Re}(\lambda_{i})\leq 0\) y cada eigenvalor con \(\text{Re}(\lambda_{i})= 0\) tiene un bloque de Jordan asociado de uno. El punto de equilibrio \(x=0\) es (globalmente) asintóticamente estable sí y sólo sí todos los eigencalores de \(A\) satisfacen \(\text{Re}(\lambda_{i})< 0\).

La demostración de este teorema se puede consultar en Khalil (2002).

Linealización

Suponga que las funciones \(f_{1}\) y \(f_{2}\) del sistema autónomo de segundo orden

(37)\[\begin{split} \begin{aligned} \dot{x}_{1} &= f_{1}(x_{1},x_{2}), \\ \dot{x}_{2} &= f_{2}(x_{1},x_{2}), \\ \end{aligned} \end{split}\]

son continuamente diferenciables y que además \(p=(p_{1},p_{2})\) es un punto de equilibrio, el sistema (37) se puede expandir mediante serie de Taylor en torno a \((p_{1},p_{2})\) como sigue

\[\begin{split} \begin{aligned} \dot{x}_{1} &= f_{1}(p_{1},p_{2}) + a_{11}(x_{1}-p_{1}) + a_{12}(x_{2}-p_{2}) + \text{H.O.T}, \\ \dot{x}_{2} &= f_{2}(p_{1},p_{2}) + a_{21}(x_{1}-p_{1}) + a_{22}(x_{2}-p_{2}) + \text{H.O.T}, \end{aligned} \end{split}\]

donde

\[\begin{split} \begin{aligned} a_{11} = \left. \frac{\partial f_{1}(x_{1},x_{2})}{\partial x_{1}} \right|_{x_{1}=p_{1},x_{2}=p_{2}}, \quad a_{12} = \left. \frac{\partial f_{1}(x_{1},x_{2})}{\partial x_{2}} \right|_{x_{1}=p_{1},x_{2}=p_{2}}, \\ a_{21} = \left. \frac{\partial f_{2}(x_{1},x_{2})}{\partial x_{1}} \right|_{x_{1}=p_{1},x_{2}=p_{2}}, \quad a_{22} = \left. \frac{\partial f_{2}(x_{1},x_{2})}{\partial x_{2}} \right|_{x_{1}=p_{1},x_{2}=p_{2}}, \end{aligned} \end{split}\]

y H.O.T. denota los términos de orden superior de la expansión de Taylor, es decir \((x_{1}-p_{1})^{2},(x_{2}-p_{2})^{2},(x_{1}-p_{1})\times (x_{2}-p_{2})\), y así sucesivamente.

Dado que \((p_{1},p_{2})\) denota el punto de equilibrio, tenemos

\[ f_{1}(p_{1},p_{2}) = f_{2}(p_{1},p_{2}) = 0. \]

Puesto que consideramos trayectorias cercanas a este punto, definimos

\[ y_{1} = x_{1} - p_{1}, \quad y_{2} = x_{2} - p_{2}. \]

Por consiguiente, las ecuaciones de estado quedan de la siguiente forma

\[\begin{split} \begin{aligned} \dot{y}_{1} &= \dot{x}_{1} = a_{11}y_{1} + a_{12}y_{2} + \text{H.O.T}, \\ \dot{y}_{2} &= \dot{x}_{2} = a_{21}y_{1} + a_{22}y_{2} + \text{H.O.T}. \end{aligned} \end{split}\]

Si consideramos una vecindad cercana al punto de equilibrio, entonces podemos decir que los términos H.O.T son despreciables y por consiguiente, realizamos una aproximación de la ecuación de estado no lineal por la ecuación de estado lineal como sigue

\[\begin{split} \begin{aligned} \dot{y}_{1} &= \dot{x}_{1} = a_{11}y_{1} + a_{12}y_{2},\\ \dot{y}_{2} &= \dot{x}_{2} = a_{21}y_{1} + a_{22}y_{2}. \\ \end{aligned} \end{split}\]

Reescribiendo lo anterior en una forma vectorial, tenemos

\[ \dot{y} = Ay, \]

donde

\[\begin{split} A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} = \left. \begin{bmatrix} \frac{\partial f_{1}}{\partial x_{1}} & \frac{\partial f_{1}}{\partial x_{2}} \\ \frac{\partial f_{2}}{\partial x_{1}} & \frac{\partial f_{2}}{\partial x_{2}} \end{bmatrix} \right|_{x=p} = \left. \frac{\partial f}{\partial x} \right|_{x=p} \end{split}\]

Note

La matrix \([\partial f/\partial x]\) es llamada la matriz Jacobiana de \(f(x)\) mientras que \(A\) es la matriz Jacobiana evaluada en el punto de equilibrio \(p\).

Ejemplo

• Considere el circuito de diodo tunel que se muestra a continuación

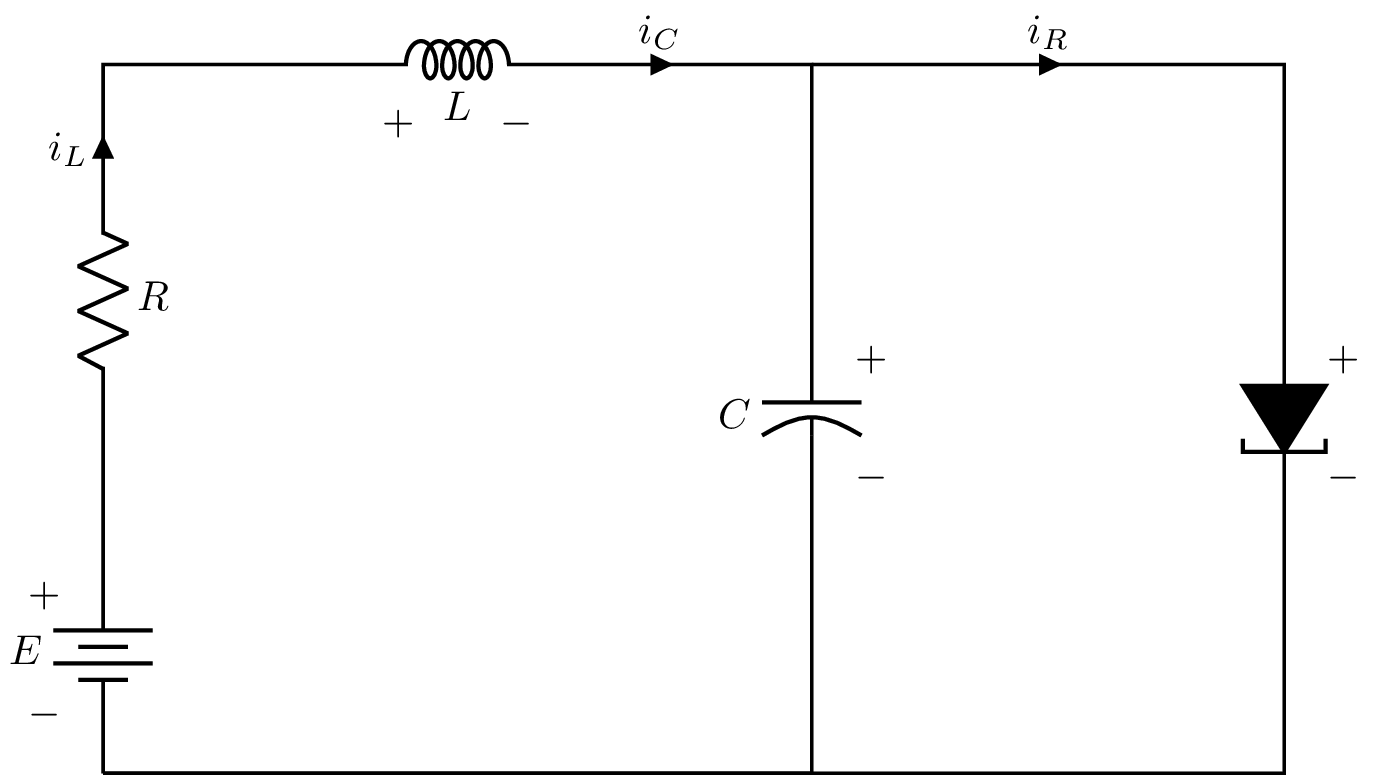
Fig. 7 Diodo túnel.

donde los elementos de almacenamiento de energía son el capacitor \(C\) y el inductor \(L\) mientras que el diodo tunel es representado por la relación \(i_{R} = h(v_{R})\). Asumiendo que los elementos del circuito son lineales e invariantes en el tiempo, el circuito de diodo tunel se puede representar matemáticamente como sigue

(38)\[\begin{split} \begin{aligned} i_{C} &= C \frac{\mathrm{d}v_{C}}{\mathrm{d}t}, \\ v_{L} &= L \frac{\mathrm{d}i_{L}}{\mathrm{d}t}, \\ \end{aligned} \end{split}\]

donde \(i\), \(v\) representan la corriente y el voltaje a través de los elementos, respectivamente.

Considere que los parámetros del modelo son \(u=1.2V\), \(R=1.5k\Omega = 1.5\times 10^{3}\Omega\), \(C=2pF = 2\times 10^{-12}F\), \(L=5\mu H = 5\times 10^{-6}H\). Además, suponga que \(h(\cdot)\) está dada por

\[ h(x_{1}) = 17.76x_{1} - 103.79x_{1}^{2} + 229.62x_{1}^{3} - 226.31x_{1}^{4} + 83.72x_{1}^{5}. \]

1. Utilice las Leyes de Kirchhoff para reescribir las ecuaciones anteriores.

2. Encuentre los puntos de equilibrio.

3. Linealice el sistema.

4. Evalúe la matriz Jacobiana en los puntos de equilibrio.

Ejemplo

• Considere el péndulo simple mostrado en la siguiente

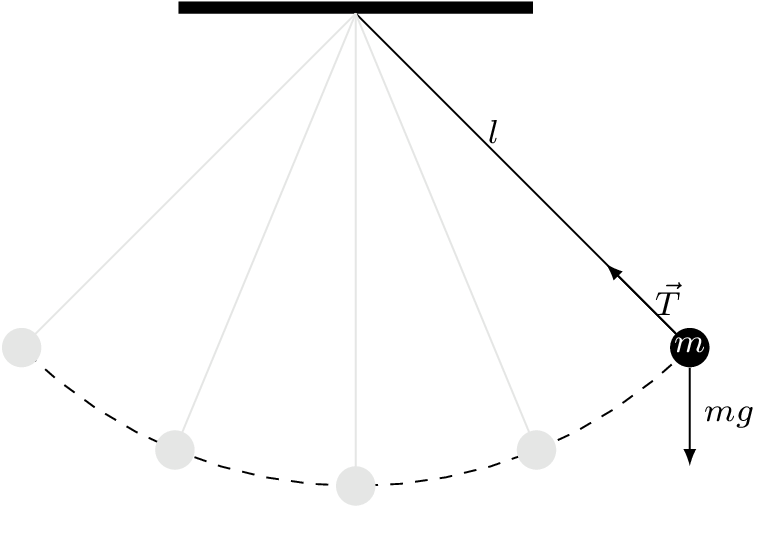
Fig. 8 Diagrama de péndulo simple sin fuerza externa.

donde \(l\) denota la longitud de la varilla, y \(m\) la masa de la bola.

Cuya representación en espacio de estados está dada como sigue

(39)\[\begin{split} \begin{aligned} \dot{x_{1}} &= x_{2}, \\ \dot{x_{2}} &= -\frac{g}{l}\sin(x_{1}) - \frac{k}{m}x_{2}. \end{aligned} \end{split}\]

1. Encuentre los puntos de equilibrio.

2. Linealice el sistema.

3. Evalúe la matriz Jacobiana en los puntos de equilibrio.

---

Análisis de la estabilidad de sistemas dinámicos linealizados

Considere un sistema LTI como se muestra en la Ec. (36) donde \(A\) es una matriz real de dimensión \(2\times 2\). La solución a este sistema con una condición inicial \(x_{0}\) está dada por la siguiente ecuación

\[ x(t) = M \exp(J_{r}t)M^{-1}x_{0}, \]

donde \(J_{r}\) es la forma real de Jordan de \(A\) y \(M\) es una matriz real no singular tal que \(M^{-1}AM = J_{r}\). Dependiendo de los eigenvalores \(\lambda_{i}\) de la matriz \(A\), la forma de Jordan puede tomar los siguientes casos

\[\begin{split} \begin{bmatrix} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{bmatrix}, \quad \begin{bmatrix} \lambda & k \\ 0 & \lambda \end{bmatrix}, \quad \begin{bmatrix} \alpha & -\beta \\ \beta & \alpha \end{bmatrix}, \end{split}\]

donde \(k\) puede tomar el valor de \(0\) o \(1\).

Caso 1. Ambos eigenvalores son reales: \(\lambda_{1} \neq \lambda_{2} \neq 0\).

El sistema tiene dos eigenvectores reales \(v_{1}\) y \(v_{2}\) asociados con \(\lambda_{1}\) y \(\lambda_{2}\), respectivamente. Donde el sistema es transformado en dos ecuaciones diferenciales de primer orden después de un cambio de coordenadas \(z=M^{-1}x\), i.e.

\[\begin{split} \begin{aligned} \dot{z}_{1} &= \lambda_{1}z_{1},\\ \dot{z}_{2} &= \lambda_{2}z_{2}, \end{aligned} \end{split}\]

cuya solución está dada como sigue, para las condiciones iniciales \((z_{10},z_{20})\)

\[ z_{1}(t) = z_{10}e^{\lambda_{1}t}, \quad z_{2}(t) = z_{20}e^{\lambda_{2}t}. \]

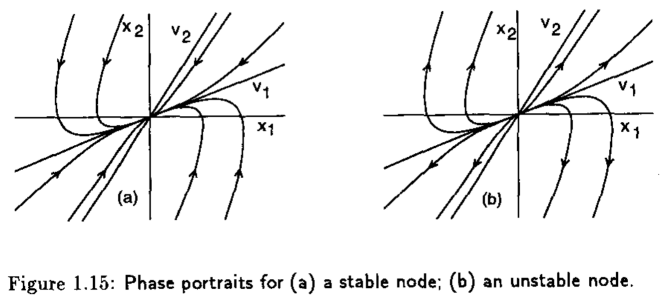
Cuando \(\lambda_{2}<\lambda_{1}<0\), el retrato fase tiene la forma de la Figura 1.15(a), donde \(x=0\) es llamado nodo estable. Por otro lado, si \(\lambda_{2}>\lambda_{1}>0\), \(x=0\), el retrato fase se muestra en la Figura 1.15(b) y se le conoce como nodo inestable.

Si el sistema tiene eigenvalores con signos opuestos, esto es \(\lambda_{2} < 0 \lambda_{1}\), decimos que \(\lambda_{2}\) es un eigenvalor estable y \(\lambda_{1}\) inestable. Por consiguiente, el retrato fase que corresponde a esta trayectoria se muestra en la Figura 1.16(a).

Caso 2. Eigenvalores complejos: \(\lambda_{1,2} = \alpha \pm j\beta\)

El sistema \(\dot{x}=Ax\) después de la transformación de coordenadas \(z = M^{-1}x\) tiene la forma

\[\begin{split} \begin{aligned} \dot{z}_{1} &= \alpha z_{1} - \beta z_{2}, \\ \dot{z}_{2} &= \beta z_{1} + \alpha z_{2}. \end{aligned} \end{split}\]

Puesto que la solución a este sistema es oscilatoria, se puede expresar en coordenadas polares como sigue

\[ r = \sqrt{z_{1}^{2} + z_{2}^{2}}, \quad \theta = \tan^{-1}\left( \frac{z_{2}}{z_{1}} \right), \]

teniendo dos ecuaciones diferenciales de primer orden desacopladas

\[\begin{split} \begin{aligned} \dot{r} &= \alpha r, \\ \dot{\theta} = \beta. \end{aligned} \end{split}\]

La solución de este sistema, para una condición inicial \((r_{0},\theta_{0})\) es

\[ r(t) = r_{0}r^{\alpha t}, \quad \theta(t) = \theta_{0} + \beta_{t}. \]

Dependiendo del valor de \(\alpha\), el retrato fase puede tomar alguna de las siguientes formas

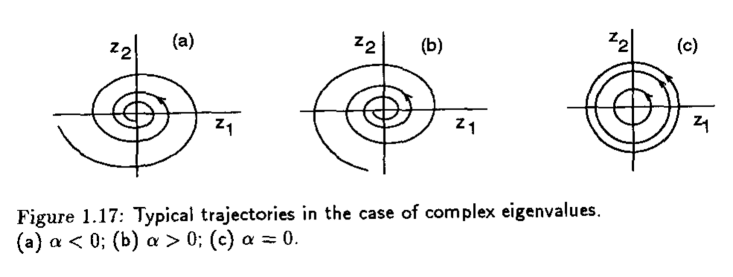
Note

El punto de equilibrio \(x=0\) es un foco estable si \(\alpha<0\), foco inestable si \(\alpha>0\) y centro si \(\alpha=0\) como se muestra a continuación

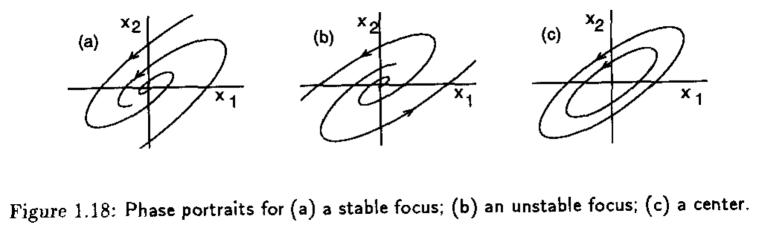
Caso 3. Eigenvalores múltiples diferentes de cero: \(\lambda_{1}=\lambda_{2} = \lambda \neq 0\)

Para este caso, el sistema \(\dot{x}=Ax\) después de un cambio de coordenadas toma la siguiente forma

\[\begin{split} \begin{aligned} \dot{z}_{1} &= \lambda z_{1} + kz_{2}, \\ \dot{z}_{2} &= \lambda z_{2}, \end{aligned} \end{split}\]

cuya solución, con c.i. \((z_{10},z_{20})\) está dada como sigue

\[ z_{1}(t) = e^{\lambda t} \left( z_{10} + kz_{20}t \right), \quad z_{2}(t) = e^{\lambda t}z_{20}. \]

Los retrato fase para este caso, considerando \(k=0\) y \(k=1\) se muestran en la siguiente figura

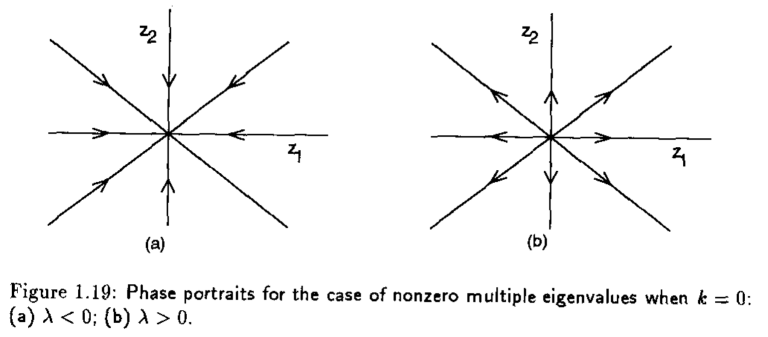
Aquí, el punto de equilibrio \(x=0\) se le conoce como nodo estable si \(\lambda < 0\) y nodo inestable si \(\lambda >0\). Las trayectorias se muestran en la siguiente representación

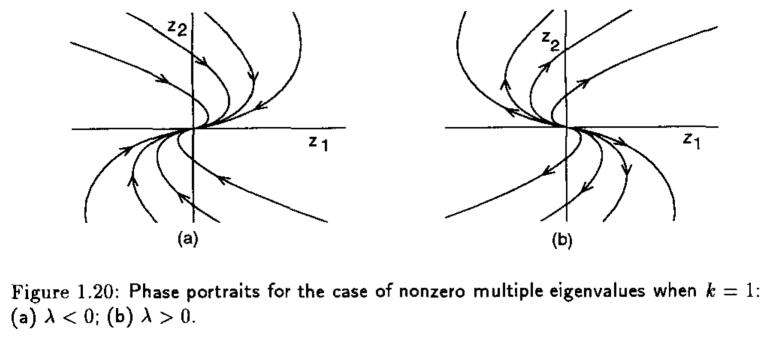
Caso 4. Uno o ambos autovalores son cero

Cuando \(\lambda_{1}=0\) y \(\lambda_{2}\neq 0\), el sistema después de una transformación de coordenadas tiene la siguiente representación

\[\begin{split} \begin{aligned} \dot{z}_{1} &= 0, \\ \dot{z}_{2} &= \lambda_{2} z_{2}, \end{aligned} \end{split}\]

cuya solución es

\[ z_{1}(t) = z_{10}, \quad z_{2}(t) = z_{20}e^{\lambda_{2}t}. \]

Cuano ambos eigenvalores se encuentran en el origen y se aplica una transformación del coordenadas al sistema \(\dot{x}=Ax\), tenemos

\[\begin{split} \begin{aligned} \dot{z}_{1} &= z_{2}, \\ \dot{z}_{2} &= 0, \end{aligned} \end{split}\]

cuya solución está dada como sigue

\[ z_{1}(t) = z_{10} + z_{20}t, \quad z_{2}(t) = z_{20}. \]

Las trayectorias que forman el retrato fase para estos casos en particular se muestran en la siguientes figuras

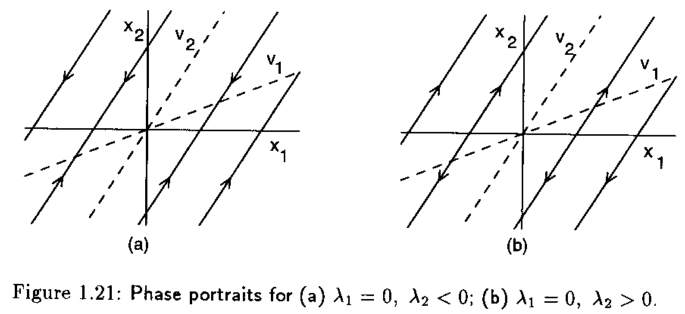
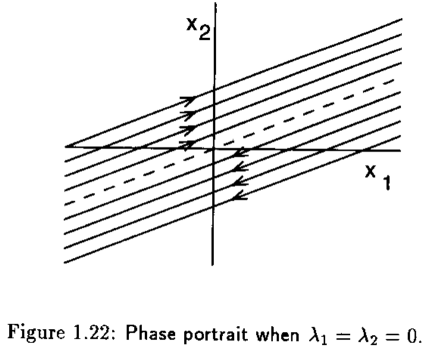
Ejemplo

• Clasifique los puntos de equilibrio del circuito de diodo tunel (38) y determine su estabilidad.

Ejemplo

• Clasifique los puntos de equilibrio del sistema de péndulo simple (39) y determine su estabilidad.

---

Análisis de estabilidad por el método directo de Lyapunov

Aleksandr Mikhailovich Lyapunov en 1892 presentó dos métodos para determinar la estabilidad de sistemas dinámicos representados en ecuaciones diferenciales ordinarias (ODEs).

El primer método utiliza la forma explícita de la solución de las ODEs para realizar el análisis de estabilidad mientras que el segundo método determina la estabilidad del sistema sin resolver las ecuaciones de estado.

Sea \(V:D\rightarrow R\) una función continuamente diferenciable definida en un dominio \(D\subset R^{n}\) que contiene el origen, entonces la derivada de \(V\) sobre la trayectoria del sistema autónomo \(\dot{x}=f(x)\), denotada por \(\dot{V}(x)\) está dada como sigue

\[\begin{split} \begin{aligned} \dot{V}(x) &= \sum_{i=1}^{n} \frac{\partial V}{\partial x_{i}} \dot{x}_{i} = \sum_{i=1}^{n} \frac{\partial V}{\partial x_{i}}f_{i}(x), \\ &= \begin{bmatrix} \frac{\partial V}{\partial x_{1}}, & \frac{\partial V}{\partial x_{2}}, & \dots, & \frac{\partial V}{\partial x_{n}} \end{bmatrix} \begin{bmatrix} f_{1}(x) \\ f_{2}(x) \\ \vdots \\ f_{n}(x) \end{bmatrix} = \frac{\partial V}{\partial x}f(x). \end{aligned} \end{split}\]

Normalmente las funciones utilizadas son funciónes reales de variable vectorial. También es posible utilizar funciones integrales pero nos vamos a centrar en las primeras.

Definition 2

Una función \(V\) es definida positiva si \(V(x)>0 ~ \forall x\neq 0\) y \(V(0)=0\).

Ejemplos

• \(V(x) = x_{1}^{2} + 2x_{2}^{2}\)

• \(V(x) = x_{1}^{2} + \frac{2x_{2}^{2}}{1+x_{2}^{2}}\)

Definition 3

Una función \(V\) es definida negativa si \(V(x)<0 ~ \forall x\neq 0\) y \(V(0)=0\).

Ejemplo

• \(V(x) = - x_{1}^{2} - \left(3x_{1}+2x_{2}\right)^{2}\)

Definition 4

Una función \(V\) es semidefinida positiva si \(V(x)\geq0 ~ \forall x\) y \(V(x)=0\).

Ejemplo

• \(V(x) = \left(x_{1} + x_{2} \right)^{2}\).

Definition 5

Una función \(V\) es semidefinida negativa si \(-V(x)\) es semidefinida positiva, i.e. \(-V(x)\geq0 ~ \forall x\) y \(V(x)=0\).

Ejemplo

• \(V(x) = -\left(x_{1} + x_{2}\right)^{2}\)

Note

\(\dot{V}(x)\) es diferente para cada sistema y además, si \(\Phi(t;x)\) es la solución al sistema \(\dot{x}=f(x)\) con valor inicial \(x\) en \(t=0\), entonces

\[ \dot{V}(x) = \frac{\mathrm{d}}{\mathrm{d}t}V\left.\left(\Phi(t;x)\right)\right|_{t=0}. \]

Ejemplo

• Considere la siguiente función

\[ V(x) = \left(x_{1} + x_{2} \right)^{2}. \]

Ejemplo

• Considere la siguiente función y determine si es definida positiva o semidefinida positiva

\[ V(x) = x_{1}^{2} + x_{2}^{2} + 1. \]

Ejemplo

• Considere la siguiente función y determine si es definida negativa

\[ V(x) = - x_{1}^{2} - \left(3x_{1}+2x_{2}\right)^{2} \]

Ejemplo

• Considere la siguiente función

\[ V(x) = x_{1}x_{2} + x_{2}^{2} \]

Formas cuadráticas

Una forma general de tener funciones \(V(x)\) es utilizando la forma cuadrática. Por ejemplo

\[\begin{split} \begin{aligned} V(x) &= \begin{bmatrix} x_{1} & x_{2} & \cdots & x_{n} \end{bmatrix} \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1n} \\ p_{12} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ p_{1n} & p_{2n} & \cdots & p_{nn} \\ \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} &=x^{T}Px \end{aligned}, \end{split}\]

donde \(P\) es una matriz simétrica. Es decir \(P = P^{T}\). O bien, de la forma hermitiana

\[\begin{split} \begin{aligned} V(x) &= \begin{bmatrix} \bar{x}_{1} & \bar{x}_{2} & \cdots & \bar{x}_{n} \end{bmatrix} \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1n} \\ \bar{p}_{12} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ \bar{p}_{1n} & \bar{p}_{2n} & \cdots & p_{nn} \\ \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} &=x^{\star}Px \end{aligned}. \end{split}\]

Ejemplo

• Considere la siguiente función en forma cuadrática y determine si es definida positiva

\[\begin{split} \begin{aligned} V(x) &= x^{T}Px \\ &= \begin{bmatrix} x_{1} & x_{2} \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \\ &= \begin{bmatrix} x_{1} + 2x_{2} & 2x_{1} + 3x_{2} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \\ &= x_{1}^{2} + 2x_{1}x_{2} + 2x_{1}x_{2} + 3x_{2}^{2} \\ &= x_{1}^{2} + 4x_{1}x_{2} + 3x_{2}^{2} \end{aligned}. \end{split}\]

Criterio de Sylvester

Una función \(V(x)\) en forma cuadrática

\[\begin{split} p_{11} > 0, \quad \left| \begin{matrix} p_{11} & p_{12} \\ {p}_{12} & p_{22} \end{matrix} \right| > 0, \quad \left| \begin{matrix} p_{11} & p_{12} & \cdots & p_{1n} \\ p_{12} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ p_{1n} & p_{2n} & \cdots & p_{nn} \\ \end{matrix} \right| > 0 \end{split}\]

o hermitiana

\[\begin{split} p_{11} > 0, \quad \left| \begin{matrix} p_{11} & p_{12} \\ \bar{p}_{12} & p_{22} \end{matrix} \right| > 0, \quad \left| \begin{matrix} p_{11} & p_{12} & \cdots & p_{1n} \\ \bar{p}_{12} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ \bar{p}_{1n} & \bar{p}_{2n} & \cdots & p_{nn} \\ \end{matrix} \right| > 0 \end{split}\]

es definida positiva si todas las menores principales sucesivas de \(P\) son positivas.

Ejemplo

• Considere la siguiente matriz \(P\)

\[\begin{split} P = \begin{bmatrix} 1 & 6 & -1 \\ 2 & 4 & 0 \\ -2 & 3 & 7 \end{bmatrix} \end{split}\]

Ejemplo

• Considere la siguiente función y determine si es definida positiva

\[ V(x) = 10x_{1}^{2} + 4x_{2}^{2} + x_{3}^{2} + 2x_{1}x_{2} - 2x_{2}x_{3} - 4x_{1}x_{3} \]

Principio del Teorema de Estabilidad de Lyapunov

Un sistema es estable si su \(E\) -energía- total (una función definida positiva) es continuamente decreciente (la derivada en el tiempo de la \(E\) total es definida negativa) hasta que alcanza un estado de equilibrio. En otras palabras, un sistema es estable si su \(E\) total se va perdiendo con el paso del tiempo.

Theorem 7 (Teorema de estabilidad de Lyapunov)

Sea \(x=0\) un punto de equilibrio para el sistema \(\dot{x}=f(x)\) y \(D\subset R^{n}\) un dominio que contiene \(x=0\), entonces \(V:D\rightarrow R\) es una función continuamente diferenciable tal que

\[ V(0) = 0, \]

\[ V(x) > 0 \text{ en } D-\{0\}, \]

\[ \dot{V}(x) \leq 0 \text{ en } D. \]

Entonces, \(x=0\) es estable. Además, si

\[ \dot{V}(x) <0 \text{ en } D-\{0\}, \]

entonces \(x=0\) es asintóticamente estable.

La demostración de este teorema se puede consultar en Khalil (2002).

Función candidata de Lyapunov

Es aquella función que se propone para poder realizar el análisis de estabilidad de Lyapunov. Recordemos que anteriormente trabajamos con funciones definidas positivas y cómo verificar que cumplieran con la definición mas no con funciones candidatas de Lyapunov.

En términos estrictos, una función candidata de Lyapunov es una función definida positiva. Esta función definida positiva puede ser de manera local o global. En nuestro caso, consideramos que es local. Esto es

\[ V(0) = 0 \]

\[ V(x) >0 ~ \forall x \in U\backslash \{0\} \]

donde \(U\) denota un conjunto del espacio de estados y \(\backslash \{0\}\) significa excepto en el origen.

Note

Recordemos que el valor \((0,0)\) se refiere al origen del sistema que puede ser un punto de equilibrio. Cuando linealizamos un sistema no lineal en un punto de equilibrio que no sea el origen, entonces el origen del sistema lineal es el punto de equilibrio del sistema lineal.

Ejemplo

• Considere el siguiente sistema, y verifique si es estable o no en el sentido de Lyapunov

\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2} - x_{1}(x_{1}^{2} + x_{2}^{2}),\\ \dot{x}_{2} &= -x_{1} - x_{2}(x_{1}^{2} + x_{2}^{2}). \end{aligned} \end{split}\]

Ejemplo

• Considere el sistema de péndulo simple sin fricción

\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= - \frac{g}{l}\sin\left(x_{1}\right), \end{aligned} \end{split}\]

donde \(x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix}\).

Theorem 8

Sea \(x=0\) un punto de equilibrio para el sistema \(\dot{x} = f(x)\) y \(V:\mathbb{R}^{n}\rightarrow \mathbb{R}\) una función continuamente diferenciable tal que

\[ V(0) = 0, \quad V(x)>0, \quad \forall x \neq 0, \]

\[ \|x\| \rightarrow \infty \Rightarrow V(x) \rightarrow \infty, \]

\[ \dot{V}(x)<0, \forall x\neq 0, \]

entonces \(x=0\) es globalmente asintóticamente estable.

Ejemplo

• Considere el siguiente sistema no lineal escalar

\[ \begin{aligned} \dot{x} = \frac{2}{1+x}-x. \end{aligned} \]

Ejemplo

• Considere las ecuaciones que caracterizan un modelo para un péndulo colgante

\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= -\sin(x_{1}), \\ \end{aligned} \end{split}\]

donde \(x_{1}\) denota el ángulo entre el péndulo y la vertical con \(x_{1}>0\) corresponde a la rotación en sentido contrario a las manecillas del reloj.