Modelo NARMAX

Metodología

Los pasos a seguir para alcanzar el objetivo son los siguientes:

1. Importación de la base de datos.

2. Análisis de las variables para identificar el tipo de dato.

3. Verificación de valores NaN o Nulos.

4. Distribución de las variables.

5. Cálculo de la matriz de correlación.

6. Procesamiento de datos.

7. Resultados y discusión.

Configuración

Importación de librerías

Importamos todas las librerías necesarias para trabajar

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sysidentpy.model_structure_selection import FROLS
from sysidentpy.basis_function._basis_function import Polynomial
from sysidentpy.utils.display_results import results
from sysidentpy.utils.plotting import plot_residues_correlation, plot_results
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.generate_data import get_miso_data
from sysidentpy.residues.residues_correlation import (compute_residues_autocorrelation, compute_cross_correlation,)

Importación de datos

Importamos la base de datos para trabajar el problema de regresión

# 1. Importación de la base de datos
db_ballbeam = pd.read_csv('datasets/ballbeam.csv')
db_ballbeam.head()

	angle	position
0	-0.001963	-0.004885
1	-0.001963	-0.004641
2	-0.001963	-0.003786
3	-0.001963	-0.004030
4	-0.001963	-0.003908

# 2. Análisis de las variables para identificar el tipo de dato
db_ballbeam.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 2 columns):
 #   Column    Non-Null Count  Dtype  
---  ------    --------------  -----  
 0   angle     1000 non-null   float64
 1   position  1000 non-null   float64
dtypes: float64(2)
memory usage: 15.8 KB

# 3. Verificación de valores NaN o nulos
db_ballbeam.isnull().sum()

angle       0
position    0
dtype: int64

# 6. Procesamiento de datos
# Antes de generar un modelo de regresión lineal debemos representar los datos para observar si existe una relación. 
# Además, dicha relación debe ser cuantificada mediante un coeficiente de correlación
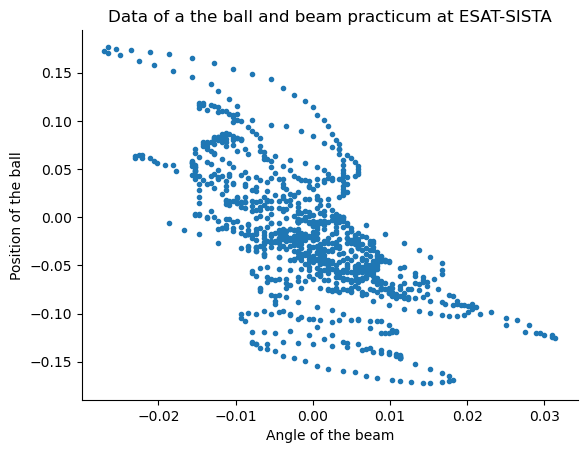
plt.plot(db_ballbeam['angle'], db_ballbeam['position'],'.')
plt.xlabel("Angle of the beam")
plt.ylabel("Position of the ball")
plt.title('Data of a the ball and beam practicum at ESAT-SISTA')

Text(0.5, 1.0, 'Data of a the ball and beam practicum at ESAT-SISTA')

scaler = preprocessing.MinMaxScaler(feature_range = (0.1, 0.9))         

X = scaler.fit_transform(np.array(db_ballbeam['angle']).reshape(-1,1))
y = scaler.fit_transform(np.array(db_ballbeam['position']).reshape(-1,1))

# Libreria para divir el conjunto de datos experimentales en subconjuntos
from sklearn.model_selection import train_test_split

# El tamanio de la prueba especifica la cantidad de datos que desea reservar para el conjunto de prueba.
# El parametro Random_state es solo una semilla aleatoria que podemos usar.
# Puede usarlo si desea reproducir estos resultados especificos.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.40, random_state = 696)

X_train = np.array(X_train).reshape(-1, 1)
X_test = np.array(X_test).reshape(-1, 1)
y_train = np.array(y_train).reshape(-1, 1)
y_test = np.array(y_test).reshape(-1, 1)

basis_function = Polynomial(degree = 4)

model = FROLS(order_selection = True,  n_info_values = 3, extended_least_squares = False, ylag = 4, xlag = 10, info_criteria = "aic", estimator = "least_squares", basis_function = basis_function, )

model.fit(X = X_train, y = y_train)
yhat = model.predict(X = X_test, y = y_test)
rrse = root_relative_squared_error(y_test, yhat)
print(rrse)

4.620230314545616

r = pd.DataFrame( results( model.final_model, model.theta, model.err, model.n_terms, err_precision=8, dtype="sci", ), columns=["Regressors", "Parameters", "ERR"], )
print(r) 

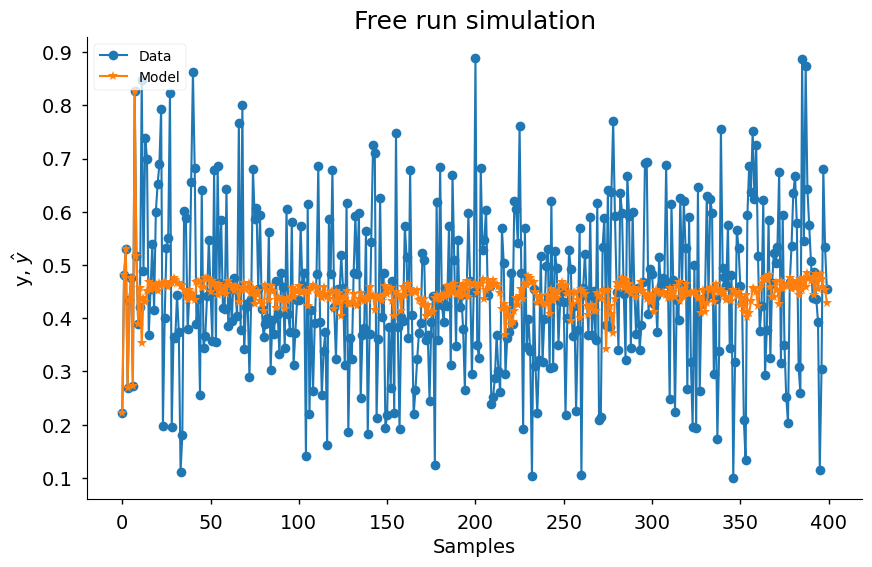
plot_results(y = y_test, yhat = yhat, n = 1000, style = "seaborn-v0_8-notebook")
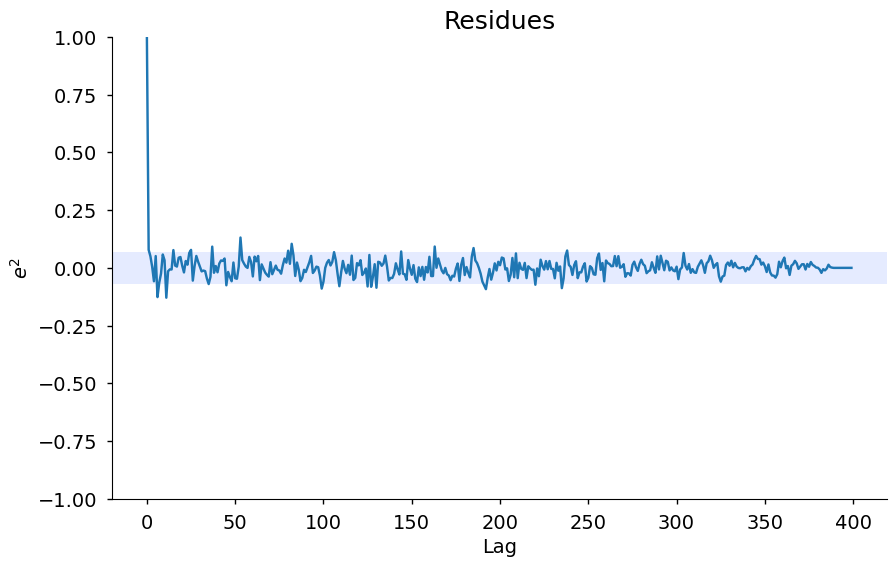
ee = compute_residues_autocorrelation(y_test, yhat)
plot_residues_correlation(data = ee, title = "Residues", ylabel="$e^2$", style = "seaborn-v0_8-notebook")
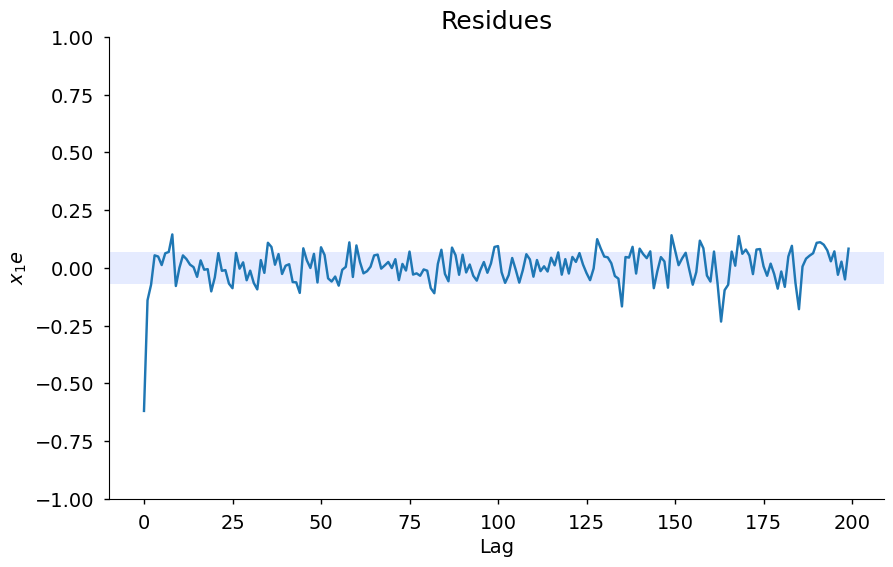
x1e = compute_cross_correlation(y_test, yhat, X_test[:, 0])
plot_residues_correlation(data = x1e, title = "Residues", ylabel = "$x_1e$", style = "seaborn-v0_8-notebook")

                     Regressors   Parameters             ERR
0                             1   4.9092E-01  8.96501506E-01
1       x1(k-10)x1(k-8)^2y(k-4)  -4.8030E-01  1.06398371E-03
2  x1(k-7)x1(k-6)x1(k-4)x1(k-3)  -4.7516E-01  6.56353610E-04

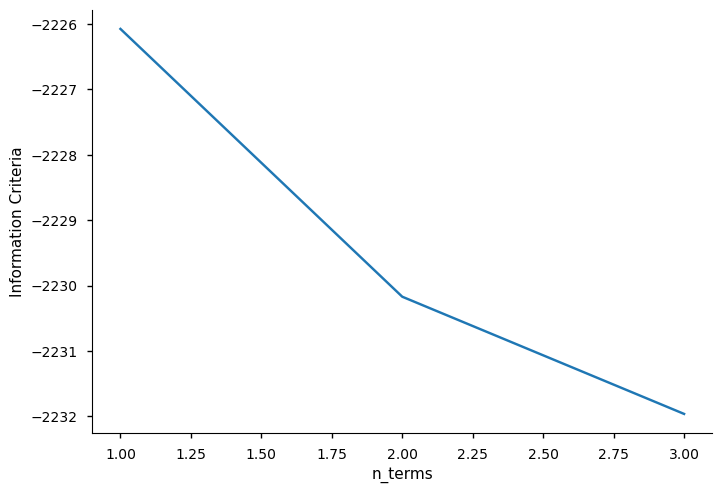
xaxis = np.arange(1, model.n_info_values + 1)
plt.plot(xaxis, model.info_values)
plt.xlabel("n_terms")
plt.ylabel("Information Criteria")

Text(0, 0.5, 'Information Criteria')