Controlabilidad de sistemas dinámicos

Concepto de controlabilidad

Considere un sistema \(n\)-dimensional en representación de espacio-estado

(40)\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx + Du, \end{aligned} \end{split}\]

donde \(A\), \(B\), \(C\) son matrices de dimensión \(n\times n\), \(n\times 1\), y \(1\times n\), respectivamente. Además, \(D\) es escalar.

Definition 6

El sistema (40) es controlable si cualquier estado se puede transferir a cualquier otro estado en un tiempo finito aplicando una entrada.

Theorem 9

Para cada \(y\), existe una solución \(x\) en \(Ax=y\) si y sólo si \(A\) es de rango completo.

Recordemos que la solución al sistema (40) dado una entrada \(u(t)\) y una c.i. \(x(0)\) está dado como sigue

(41)\[ x(t) = \underbrace{e^{At}x(0)}_{\text{Zero-Input Response}} + \underbrace{e^{At}\int_{0}^{t} e^{-A\tau}Bu(\tau)\mathrm{d}\tau}_{\text{Zero-State Response}}, \]

y

\[ y(t) = ce^{At}x(0) + ce^{At}\int_{0}^{t}e^{-A\tau}Bu(\tau)\mathrm{d}\tau + Du(t). \]

Reescribiendo (41), tenemos

\[\begin{split} \begin{aligned} x(t) - e^{At}x(0) &= \int_{0}^{t} \left[ I + A(t-\tau) + A^{2}\frac{(t-\tau)^{2}}{2} + \cdots \right] Bu(\tau)\mathrm{d}\tau, \\ &= B \int_{0}^{t}u(\tau)\mathrm{d}\tau + AB \int_{0}^{t}(t - \tau)u(\tau)\mathrm{d}\tau \\ &+ A^{2}B \int_{0}^{t} \frac{1}{2}(t-\tau)^{2}u(\tau)\mathrm{d}\tau + \cdots, \\ &= \begin{bmatrix} B & AB & A^{2}B \cdots \end{bmatrix} \begin{bmatrix} \int_{0}^{t}u(\tau)\mathrm{d}\tau \\ \int_{0}^{t}(t-\tau)u(\tau)\mathrm{d}\tau \\ \int_{0}^{t}\frac{1}{2}(t-\tau)^{2}u(\tau)\mathrm{d}\tau \\ \vdots \end{bmatrix} \end{aligned} \end{split}\]

Utilizando el Theorem 9, tenemos que para cualquier \(x(0)\) y \(x(t)\), una solución \(u(t)\) existe si y sólo si la matriz

(42)\[ \begin{bmatrix} B & AB & A^{2}B & \cdots & A^{n-1}B & \cdots \end{bmatrix} \]

tiene rango \(n\).

Utilizando el teorema de Cayley-Hamilton, la matriz (42) tiene rango \(n\) si y sólo si la matriz \(n\times n\)

(43)\[ U = \begin{bmatrix} B & AB & A^{2}B & \cdots & A^{n-1}B \end{bmatrix} \]

tiene rango \(n\).

En resumen, el sistema (40) es controlable si la matriz (43) tiene rango \(n\), o bien, \(\text{det}\{U\} \neq 0\).

Note

La matriz (43) es llamada matriz de controlabilidad.

Ejemplo

• Considere la siguiente función de transferencia

\[ G(s) = \frac{N(s)}{D(s)} = \frac{2s-1}{s^{2}-1.5s-1} = \frac{2s-1}{(s-2)\left(s+\frac{1}{2}\right)} \]

Ejemplo

• Considere la siguiente función de transferencia

\[ G(s) = \frac{N(s)}{D(s)} = \frac{2s+1}{s^{2}-1.5s-1} = \frac{2s+1}{(s-2)\left(s+\frac{1}{2}\right)} \]

Ejemplo

• Considere el sistema de equilibrio que se muestra en la siguiente Figura.

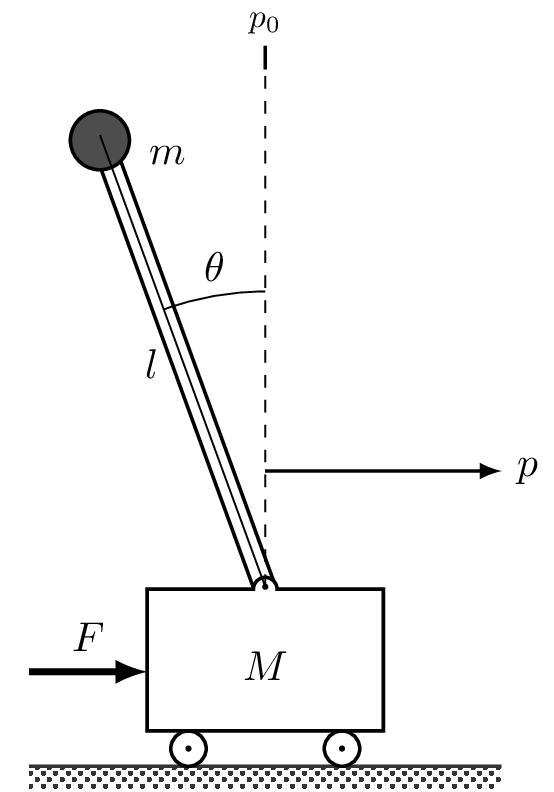
Fig. 9 Modelo del sistema carro-péndulo.

En este ejemplo, el centro de masa se equilibra por encima de un punto de pivote. Un ejemplo de ello se puede ver en la película “Guardia de supermercado”.

Fig. 10 Paul Blart. Guardia de supermercado.

El modelo no lineal para el sistema de equilibrio se muestra a continuación

\[\begin{split} \begin{aligned} (M + m)\ddot{p} - ml \cos(\theta)\ddot{\theta} &= -c\dot{p} - ml \sin(\theta)\dot{\theta}^{2} + F, \\ (J + ml^{2})\ddot{\theta} - ml\cos(\theta)\ddot{p} &= -\gamma \dot{\theta} + mgl\sin(\theta), \end{aligned} \end{split}\]

donde \(M\) es la masa de la base, \(m\) y \(J\) la masa y el momento de inercia del sistema a ser balanceado. Además, \(l\) denota la distancia de la base al centro de masa del cuerpo balanceado, \(c\) y \(\gamma\) son los coeficientes de fricción viscosa así como \(g\) representa la aceleración debido a la gravedad.

La dinámica del sistema en espacio de estado se puede obtener considerando como variables de estado\(x = (p,\theta,\dot{p},\dot{\theta})\), la entrada como \(u=F\) y salida como \(y=(p,\theta)\).

Si definimos la masa total y la inercia total como sigue, tenemos

\[ M_{t} = M + m, \quad J_{t} = J + ml^{2}. \]

Por consiguiente, podemos representar las ecuaciones de movimiento como sigue

\[\begin{split} \begin{bmatrix} \dot{p} \\ \dot{\theta} \\ \ddot{p} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{p} \\ \dot{\theta} \\ \frac{-mls_{\theta}\dot{\theta}^{2} + mg(ml^{2}/J_{t})s_{\theta}c_{\theta} - c\dot{p} - \gamma l m c_{\theta}\dot{\theta} + u}{M_{t} - m(ml^{2}/J_{t})c_{\theta}^{2}}\\ \frac{-ml^{2}s_{\theta}c_{\theta}\dot{\theta}^{2} + M_{t}gls_{\theta} - cl c_{\theta} \dot{p} - \gamma(M_{t}/m)\dot{\theta} + lc_{\theta}u}{J_{t}(M_{t}/m) - m(lc_{\theta})^{2}} \end{bmatrix}, \end{split}\]

\[\begin{split} y = \begin{bmatrix} p \\ \theta \end{bmatrix}, \end{split}\]

donde \(c_{\theta} = \cos(\theta)\) y \(s_{\theta} = \sin(\theta)\).

En ocaciones, el ángulo \(\theta\) puede ser cercano a \(0\). Por consiguiente, podemos hacer las siguientes suposiciones: \(\sin(\theta) \approx \theta\) y \(\cos(\theta) \approx 1\). Además, si \(\dot{\theta}\) es pequeño, entonces se puede menospreciar los términos cuadráticos y superiores en \(\dot{\theta}\).

Reescribiendo el sistema a partir de estas suposiciones, tenemos

(44)\[\begin{split} \begin{bmatrix} \dot{p} \\ \dot{\theta} \\ \ddot{p} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & m^{2}l^{2}g/\mu & -cJ_{t}/\mu & -\gamma J_{t}lm/\mu \\ 0 & M_{t}mgl/\mu & -clm/\mu & -\gamma M_{t}/\mu \end{bmatrix} \begin{bmatrix} p \\ \theta \\ \dot{p} \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ J_{t}/\mu \\ lm/\mu \end{bmatrix}u, \end{split}\]

\[\begin{split} y = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix}x, \end{split}\]

donde \(\mu = M_{t}J_{t} - m^{2}l^{2}\). Además, considere \(c = \gamma = 0\).

Ejemplo

• El péndulo invertido es una variación del sistema mostrado en el ejemplo anterior. La diferencia radica en que la base \(p\) no necesita estar controlada y lo único que se desea es estabilizar la horientación vertical de la barra. Este sistema se puede apreciar en la siguiente Figura.

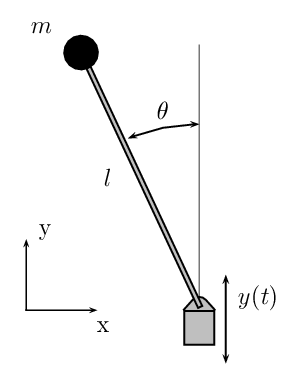
Fig. 11 Sistema de péndulo invertido.

El sistema de ecuaciones que describe la dinámica del péndulo simple está dado como sigue

\[\begin{split} \begin{bmatrix} \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{\theta} \\ \frac{mgl}{J_{t}}\sin(\theta) - \frac{\gamma}{J_{t}}\dot{\theta} + \frac{l}{J_{t}}\cos(\theta)u \end{bmatrix}, \quad y = \theta, \end{split}\]

donde \(\gamma\) es el coeficiente de fricción rotacional, \(J_{t} = J + ml^{2}\) y \(u\) es la fuerza aplicada a la base.

---

Formas canónicas de controlabilidad

Considere el caso general representado en función de transferencia

\[ G(s) = \frac{N(s)}{D(s)} = \frac{b_{1}s^{3} + b_{2}s^{2} + b_{3}s + b_{4}}{s^{4} + a_{1}s^{3} + a_{2}s^{2} + a_{3}s + a_{4}}. \]

La forma de realización controlable del sistema anterior es

\[\begin{split} \begin{aligned} \dot{x} &= \begin{bmatrix} -a_{1} & -a_{2} & -a_{3} & -a_{4} \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} x + \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}u, \\ y &= \begin{bmatrix} b_{1} & b_{2} & b_{3} & b_{4} \end{bmatrix}x, \end{aligned} \end{split}\]

donde la matriz de controlabilidad puede ser obtenida como sigue

(45)\[\begin{split} U = \begin{bmatrix} 1 & -a_{1} & e_{2} & e_{3} \\ 0 & 1 & -a_{1} & e_{2} \\ 0 & 0 & 1 & -a_{1} \\ 0 & 0 & 0 & 1 \end{bmatrix}, \end{split}\]

con \(e_{2} := -a_{2} + a_{1}^{2}\) y \(e_{3} := -a_{3} + 2a_{1}a_{2}-a_{1}^{3}\).

Note

La matriz (45) es una matriz triangular cuyo determinante siempre es 1. Por consiguiente, siempre es controlable y es la razón por la que se llama forma controlable.

---

Estabilización por retroalimentación de estado

Supongamos que se desea controlar un sistema en representación de espacio de estados lineal. Por simplicidad consideramos que tiene una sola entrada y que la ley de control de retroalimentación parte de la idea de que el sistema en lazo cerrado tiene eigenvalores deseados.

El diagrama mostrado en la Fig. 12 representa un sistema de control que usa retroalimentación de estado. Este sistema constan de un proceso representado por un modelo lineal, los elementos del control denotados por \(K\) y \(k_{r}\), una señal de referencia \(r\) y perturbaciones \(d\). El objetivo de control por retroalimentación es regular la salida del sistema.

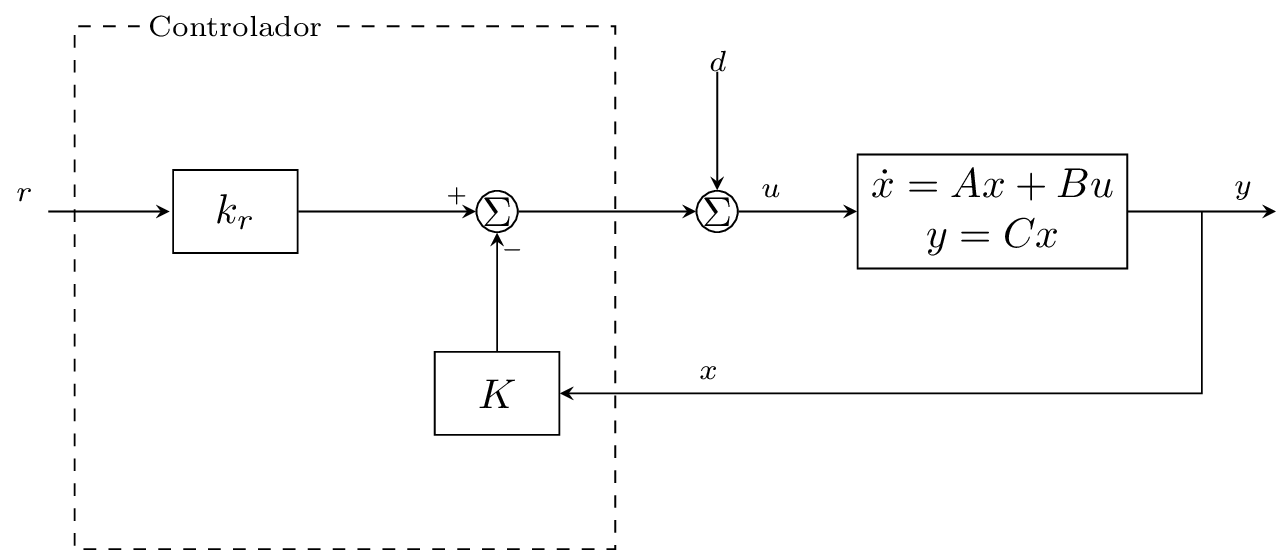
Fig. 12 Sistema de control con retroalimentación de estado donde el controlador utiliza el estado \(x\), la entrada de referencia \(r\) y la entrada \(u\). Aquı́ la perturbación está dada a través de \(d\).

Entonces, considere el siguiente sistema \(n\)-dimensional en representación de espacio-estado

(46)\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx + Du, \end{aligned} \end{split}\]

con función de transferencia

\[ G(s) = C(sI - A)^{-1}B. \]

El objetivo es llevar la salida \(y\) al valor de referencia \(r\) a partir de la medición de los estados \(x\). Para ello, consideramos que la ley de control invariante en el tiempo definida como \(u\) es una función del estado y la referencia como se muestra a continuación

(47)\[ u = r - Kx, \]

donde \(K = \begin{bmatrix} k_{1} & k_{2} & \cdots & k_{n} \end{bmatrix}\) es un vector real de dimensión \(1\times n\).

La ecuación (47) es conocida como retroalimentación de estado de ganancia constante o simplemente retroalimentación de estado [Åström and Murray, 2021].

Sustituyendo (47) en (46), tenemos

\[\begin{split} \begin{aligned} \dot{x} &= Ax - BKx + Br, \\ &= (A-BK)x + Br, \\ y &= Cx, \end{aligned} \end{split}\]

con función de transferencia

\[ G_{o}(s) = C(sI - A + Bk)^{-1}B, \]

con polinomio caracteristico

(48)\[ p(s) = s^{n} + a_{1}s^{n-1}+\cdots+a_{n-1}s + a_{n}. \]

El cálculo de la ganancia de retroalimentación \(K\) para que el sistema de lazo cerrado con polinomio (48) se conoce como asignación de eigenvalores o localización de polos.

Por otro lado, si consideramos el esquema de control mostrado en la Fig. 12, tenemos la siguiente ley de control

\[ u = -Kx + k_{r}r, \]

donde el sistema en lazo cerrado se expresa como sigue

\[\begin{split} \begin{aligned} \dot{x} &= (A-BK)x + Bk_{r}r, \\ y &= Cx. \end{aligned} \end{split}\]

Note

Es evidente que \(k_{r}\) no afecta la estabilidad del sistema ya que esta está determinada por los eigenvalores del \(A-BK\).

Los puntos de equilibrio del sistema en lazo cerrado está dado por la siguiente expresión

\[ x_{e} = - \left(A - BK \right)^{-1}Bk_{r}r, \quad y_{e} = Cx_{e}, \]

donde \(k_{r}\) es escogida tal que \(y_{e} = r\). Además, dado que \(k_{r}\) es un escalar, podemos obtenerlo a partir de la siguiente expresión

\[ k_{r} = - \frac{1}{C\left(A - BK \right)^{-1}B} \]

Procedimiento para la asignación de eigenvalores

1. Calcule el polinomio característico de \(A:\Delta (\lambda) = \text{det}(\lambda I-A)\).

2. Calcule el polinomio característico deseado

\[\begin{split} \begin{aligned} \bar{\Delta}(\lambda) &= (\lambda-\lambda_{1})(\lambda-\lambda_{2})(\lambda-\lambda_{3})\cdots (\lambda-\lambda_{n}), \\ &= \lambda^{n} + \bar{a}_{1}\lambda^{n-1} + \bar{a}_{2}\lambda^{n-2} + \dots + \bar{a}_{n}. \end{aligned} \end{split}\]

3. Calcule la ganancia de retroalimentación para la ecuación equivalente en la forma controlable

\[ \bar{k} = \begin{bmatrix} \bar{a}_{1}-a_{1} & \bar{a}_{2}-a_{2} & \cdots & \bar{a}_{n}-a_{n} \end{bmatrix}. \]

4. Calcule la transformación equivalente

\[\begin{split} S:=P^{-1} = \begin{bmatrix} B & AB & A^{2}B & A^{3}B \end{bmatrix} \begin{bmatrix} 1 & a_{1} & a_{2} & \dots & a_{n-1} \\ 0 & 1 & a_{1} & \dots & a_{n-2} \\ 0 & 0 & 1 & \dots & a_{n-3} \\ \vdots & \vdots & \vdots & \dots & \vdots \\ 0 & 0 & 0 & \dots & 1 \end{bmatrix}. \end{split}\]

5. Calcule la ganancia de retroalimentación \(k=\bar{k}P = \bar{k}S^{-1}\).

Note

Existen otras formas para obtener la ganancia de retroalimentación \(k\), una de ellas es la fórmula de Ackerman dada por la siguiente ecuación

\[ \begin{aligned} k &= \begin{bmatrix} 0 & 0 & 0 & \cdots & 1 \end{bmatrix} \begin{bmatrix} B & AB & A^{2}B & \cdots & A^{n}B \end{bmatrix}^{-1}\bar{\Delta}(A), \end{aligned} \]

donde \(\bar{\Delta}(s)\) es el polinomio característico de \((A-Bk))\), por lo tanto \(\bar{\Delta}(A) \neq 0\).

Note

Si \((A,B)\) es controlable, entonces los eigenvalores de \((A-Bk)\) pueden ser asignados arbitrariamente escogiendo una ganancia de retroalimentación real \(k\).

Ejemplo

• Considere el siguiente sistema en representación de espacio de estados

\[\begin{split} \begin{aligned} \dot{x} &= \begin{bmatrix} \dot{x}_{1} \\ \dot{x}_{2} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & -1 \end{bmatrix}x + \begin{bmatrix} 0 \\ 10 \end{bmatrix}u, \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}x \end{aligned} \end{split}\]

cuya función de transferencia es

\[ G(s) = \frac{10}{s^{2} + s}. \]

Encuentre la ganancia de retroalimentación \(k\) en \(u=r-kx\) tal que la ecuación resultante tenga sus eigenvalores en \(-2\pm j2\).

Ejemplo

• Considere el problema de regular la población de un ecosistema mediante la modulación del suministro de alimentos. Para ello considere el modelo depredador-presa cuya dinámica está dada por las siguientes ecuaciones

(49)\[\begin{split} \begin{aligned} \dot{H} &= (r + u)H\left(1 - \frac{H}{k} \right) - \frac{aHL}{c+H}, \quad H\geq 0, \\ \dot{L} &= b \frac{aHL}{c + H} - dL, \quad L \geq 0. \end{aligned} \end{split}\]

En este sistema, \(r\) denota la tasa de crecimiento de las liebres, \(k\) la población máxima, \(a\) el término que describe la disminución de las liebres en función de la población, \(c\) representa la tasa de consumo de presas, \(b\) el coeficiente de crecimiento de los linces y finalmente \(d\) la tasa de mortalidad de los linces.

Ejemplo

• Considere el problema del carro-péndulo dado por la Ec. (44)

(50)\[\begin{split} A = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & m^{2}l^{2}g/\mu & -cJ_{t}/\mu & -\gamma J_{t}lm/\mu \\ 0 & M_{t}mgl/\mu & -clm/\mu & -\gamma M_{t}/\mu \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ 0 \\ J_{t}/\mu \\ lm/\mu \end{bmatrix}, \end{split}\]

donde \(\mu = M_{t}J_{t} - m^{2}l^{2}\) y \(\gamma=c\neq0\).

Para este ejercicio, utilice los parámetros presentados en la siguiente Tabla, demuestre que el sistema es controlable y que además, es posible utilizar la estrategia de control por retroalimentación de estado para estabilidar el sistema.

Variable	Valor	Unidades
M	10	kg
m	80	kg
c	0.1	N s/m
J	100	kg m \({}^{2}\) /s \(^{2}\)
l	1	m
Y	0.01	N m s
g	9.81	m/s \({}^{2}\)

Ejemplo

• Considere un vehículo de dos ruedas como se muestra en la Fig. 13

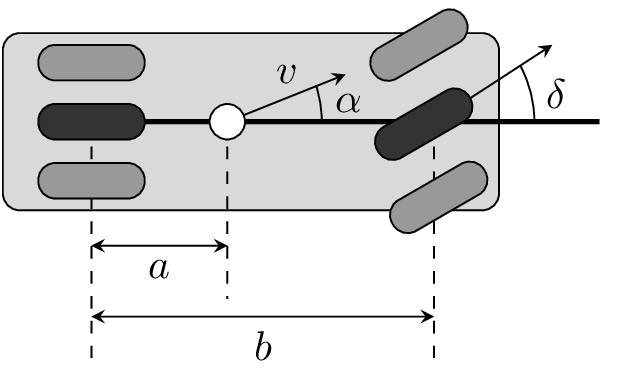
Fig. 13 Dirección del vehı́culo: modelo de bicicleta

Nuestro interés es analizar cómo la velocidad del vehículo depende del ángulo de dirección \(\delta\). Para ello, consideramos que \(v\) representa la velocidad en el centro de la masa, \(a\) la distancia de la rueda trasera, y \(b\) la base de la rueda.

Sean \(x\) e \(y\) las coordenadas del centro de masa, \(\theta\) en ángulo de rumbo y \(\alpha\) el ángulo entre el vector de velocidad \(v\) y la línea central del vehículo, entonces la relación entre \(\alpha\) y el ángulo de dirección \(\delta\) está dada como sigue

\[ \alpha(\delta) = \text{arctan}\left( \frac{a\tan(\delta)}{b} \right), \]

donde \(a := r_{a}\tan(\alpha)\), \(b:= r_{a} \tan(\delta)\).

Asuma que las ruedas no patinan y que la velocidad de las ruedas traseras es \(v_{0}\), entonces la velocidad del vehículo en su centro de masa es \(v=v_{0}/\cos(\alpha)\). Por consiguiente, el movimiento de este punto está dado como sigue

(51)\[\begin{split} \begin{aligned} \dot{x} &= v\cos(\alpha + \theta) = v_{0} \frac{\cos(\alpha + \theta)}{\cos(\alpha)}, \\ \dot{y} &= v\sin(\alpha + \theta) = v_{0} \frac{\sin(\alpha + \theta)}{\cos(\alpha)}. \end{aligned} \end{split}\]

El ángulo \(\theta\), afectado por el ángulo de dirección está dado por la siguiente relación

\[ \dot{\theta} = \frac{v_{0}}{r_{a}} = \frac{v_{0}}{b}\tan(\delta). \]

Asuma que \(\delta = 0\) y \(\dot{\theta} = 0\) para encontrar el punto de equilibrio del sistema y proceda a linealizar (51).

Respuesta de estado estacionario

Considere un sistema entrada-salida lineal como se muestra en la siguiente expresión

\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx, \end{aligned} \end{split}\]

donde su solución se puede obtener a partir de la ecuación de convolución

(52)\[ y(t) = Ce^{At}x_{0} + \int_{0}^{t}Ce^{A(t-\tau)}Bu(\tau) \mathrm{d}\tau. \]

Como se puede observar, la respuesta del sistema depende de una condición inicial \(x_{0}\) y una entrada \(u\). Además, es posible observar que en esta expresión existen dos componentes: la respuesta transitoria y la respuesta de estado estable. La primera ocurre cuando se aplica una entrada y se observa un desajuste entre la condición inicial y la solución de estado estable. La segunda refleja el comportamiento del sistema bajo las entradas dadas. En la Fig. 14 podemos ver estos dos componentes en respuesta ante una entrada de tipo escalón unitario.

Note

En la práctica, se espera que si la entrada es periódica la respuesta también lo sea. Lo mismo con entradas constantes.

Un escalón unitario, entrada escalón o escalón de Heaviside es una función definida a pedazos como sigue

(53)\[\begin{split} u(t) = \left\{ \begin{matrix} 0, & t = 0, \\ 1, & t>0. \end{matrix} \right. \end{split}\]

Definimos entonces como respuesta escalonada a la salida \(y(t)\) a partir de una condición inicial en el punto de equilibrio del sistema y una entrada \(u(t)\) de la forma (53).

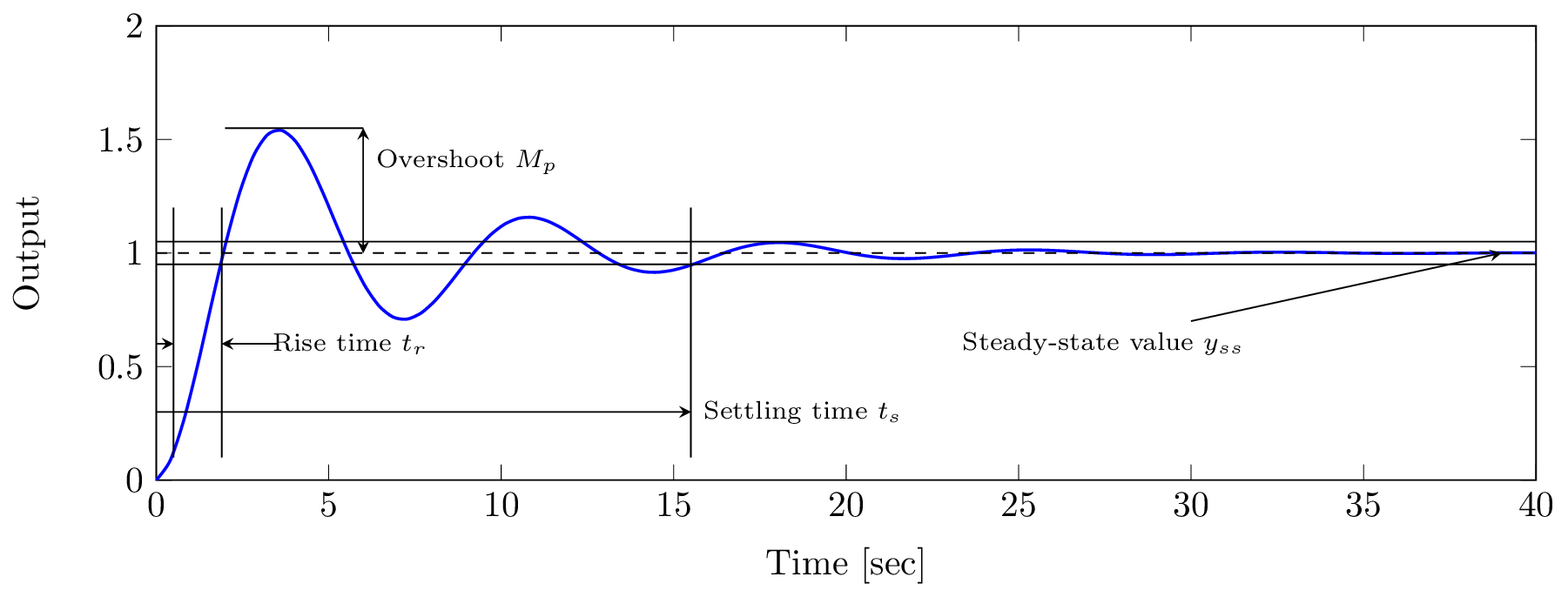
Fig. 14 Respuesta del sistema ante una entrada tipo escalón. Se observa el tiempo de subida (Rise time), sobretiro (Overshoot), tiempo de asentamiento (Settling time) y valor en estado estable (Steady-state value).

Utilizando la ecuación de convolución \eqref{eqn:conv_eq}, podemos calcular la respuesta ante una entrada tipo escalón considerando \(x_{0}=0\). Entonces, tenemos

\[\begin{split} \begin{aligned} y(t) &= \int_{0}^{t}Ce^{A(t-\tau)}Bu(\tau)\mathrm{d}\tau = C\int_{0}^{t}e^{A(t-\tau)}B\mathrm{d}\tau, \\ &= C\int_{0}^{t}e^{A\sigma}B\mathrm{d}\sigma = C\left.\left(A^{-1}e^{A\sigma}B \right)\right|^{\sigma = t}_{\sigma=0}, \\ &= CA^{-1}e^{At}B - CA^{-1}B, \end{aligned} \end{split}\]

o bien

\[ y(t) = \underbrace{CA^{-1}e^{At}B}_{\text{transitorio}} \underbrace{- CA^{-1}B}_{\text{estado estable}} \]

Velocidad de respuesta

Definimos como rendimiento transitorio a la velocidad de respuesta o la velocidad en la que el sistema alcanza al estado estable. Generalmente se especifica en términos de tiempo de levantamiento (rise time), tiempo de asentamiento (settling time) y sobretiro (overshoot). El tiempo de levantamiento lo definimos como el tiempo requerido para la respuesta pase de 0 al 90% del valor en estado estacionario como se muestra en la Fig. 14. En otras palabras, buscamos el valor más pequeño \(t_{r}\) tal que

\[ y\left(t_{r}\right) = 0.9y_{ss} \]

donde \(t_{s}\) denota el \myindex{tiempo de asentamiento}. Es decir, el tiempo que le toma a la respuesta del sistema alcanzar y mantenerse dentro del \(\pm 2\%\) de su valor en estado estable, o bien, el valor más pequeño \(t_{s}\) tal que

\[ \left|y - y_{ss} \right| \leq 0.02y_{ss}, \quad \forall~ t\geq t_{ss}. \]

Sea \(y_{\max}\) el valor máximo de \(\left|y(t) \right|,~\forall t\geq 0\) o bien

\[ y_{\max} := \max\left| y(t) \right|, \]

entonces el sobretiro se define como sigue

\[ M_{p} := \frac{y_{\max} - y_{ss}}{y_{ss}} \times 100\%. \]