Antecedentes matemáticos

Ecuaciones diferenciales no lineales

Un sistema dinámico puede ser modelado por un número finito de ecuaciones diferenciales ordinarias de primer orden acopladas como sigue

\[\begin{split} \begin{aligned} \dot{x}_{1} &= f_{1}(t,x_{1},\dots,x_{n},u_{1},\dots,u_{p}), \\ \dot{x}_{2} &= f_{2}(t,x_{1},\dots,x_{n},u_{1},\dots,u_{p}), \\ \vdots &= \vdots \\ \dot{x}_{n} &= f_{n}(t,x_{1},\dots,x_{n},u_{1},\dots,u_{p}), \\ \end{aligned} \end{split}\]

donde \(\dot{x}_{i}\) denota la derivada de \(x_{i}\) con respecto al tiempo \(t\), \(u_{1}\), \(u_{2}\), \(\dots\), \(u_{p}\) las variables de entrada o señales de control. Recordemos que las variables \(x_{1}\), \(x_{2}\), \(\dots\), \(x_{n}\) son las variables de estado.

Utilizando una notación vectorial, podemos representar el sistema anterior de la siguiente forma

\[ \dot{x} = f(t,x,u). \]

El vector de mediciones se representa como

\[ y = h(t,x,u), \]

donde \(h\) son mapeos (posiblemente no lineales) de sus argumentos a vectores de la dimensión apropiada.

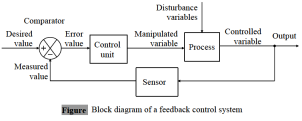
A partir de la notación anterior, podemos modelar un sistema físico como se muestra a continuación

(33)\[ \dot{x} = f(t,x). \]

Si el sistema dado en Ec. (33) contiene funciones independientes de \(t\) se dice que el sistema es autónomo de lo contrario, se dice que es no autónomo.

---

Análisis de la existencia, unicidad y continuidad de soluciones

Espacio Euclideano

Dado un conjunto de todos los vectores \(n\)-dimensionales \(x=(x_{1},\dots,x_{n})\) donde \(x_{1},\dots,x_{n}\) son números reales, define el espacio Euclidiano \(n\)-dimensional denotado por \(R^{n}\). El espacio Euclideano unidimensional consiste de todos los números reales y es denotado por \(R\).

Note

Los vectores en \(R^{n}\) se pueden sumar, multiplicar, multiplicar por un escalar y su producto interno, dados dos vectores \(x\) e \(y\) es \(x^{T}y = \sum_{i=1}^{n} x_{i}y_{i}\).

Norma vectorial y matricial

La norma \(\|x\|\) de un vector \(x\) es una función de valor real que tiene las siguientes propiedades:

• \(\|x\|\geq 0 \forall x \in R^{n}\), con \(\|x\|=0\) si y sólo si \(x=0\).

• \(\|x+y\|\leq \|x\| + \|y\| \forall x,y\in R^{n}\).

• \(\|\alpha x\| = |\alpha|\|x\| \forall \alpha \in R, x\in R^{n}\).

La norma \(p\) está definida como sigue

\[ \|x\|_{p} = \left( |x_{1}|^{p} + \cdots + |x_{n}|^{p} \right)^{1/p}, \quad 1 \leq p < \infty, \]

y

\[ \|x \|_{\infty} = \underset{i}{\max}|x_{i}|. \]

Las tres normas más utilizadas son \(\|x \|_{1}\), \(\|x \|_{\infty}\) y la norma Euclideana

\[ \|x\|_{2} = \left( |x_{1}|^{2} + \cdots + |x_{n}|^{2} \right)^{1/2} = \left( x^{T}x \right)^{1/2} \]

Funciones continuas

Una función \(f\) que mapea un conjunto \(S_{1}\) a un conjunto \(S_{2}\) se denota como \(f:S_{1}\rightarrow S_{2}\). Una función \(f:R^{n} \rightarrow R^{m}\) se dice continua e un punto \(x\) si \(f(x_{k}) \rightarrow f(x)\) cuando \(x_{k} \rightarrow x\). Equivalentemente, \(f\) es continua en \(x\) si, dado \(\varepsilon >0\), hay un \(\delta > 0\) tal que

\[ \| x - y \| < \delta \Rightarrow \| f(x) - f(y) \| < \varepsilon. \]

Una función \(f\) es continua sobre un conjunto \(S\) si esta es continua en cada punto de \(S\), y es uniformemente continua sobre S si, dado \(\varepsilon >0\) hay \(\delta >0\) (dependiente únicamente sobre \(\varepsilon\)) tal que la desigualdad se mantiene para todo \(x,y\in S\).

Note

Continuidad uniforme está definida sobre un conjunto mientras que continuidad está definida sobre un punto.

Funciones diferenciables

Una función \(f:R\rightarrow R\) es diferenciable en \(x\) si el límite

\[ \dot{f}(x) = \lim \limits_{h\rightarrow 0} \frac{f(x+h) - f(x)}{h}, \]

existe. El límite \(\dot{f}(x)\) es llamado la derivada de \(f\) en \(x\).

Una función \(f:R^{n} \rightarrow R^{m}\) es continuamente diferenciable en un punto \(x_{0}\) si las derivadas parciales \(\partial f_{i} / \partial x_{j}\) existen y son continuas en \(x_{0}\) para \(1\leq i \leq m\), \(1\leq j \leq n\).

Una función \(f\) es continuamente diferenciable sobre un conjunto \(S\) si esta es continuamente diferenciable en cada punto de \(S\). Para una función continuamente diferenciable \(f:R^{n}\rightarrow R\), el vector fila \(\partial f / \partial x\) está definido por

\[ \frac{\partial f}{\partial x} = \left[\frac{\partial f}{\partial x_{1}},\dots,\frac{\partial f}{\partial x_{n}} \right]. \]

El vector gradiente, denotado por \(\nabla f(x)\) es

\[ \nabla f(x) = \left[ \frac{\partial f}{\partial x} \right]^{T}. \]

La matriz Jacobiana \(\left[\partial f/\partial x \right]\) es una matriz \(m\times n\) cuyo elemento en la \(i\)-ésima fila y la \(j\)-ésima columna es \(\partial f_{i}/\partial x_{j}\) para una función continuamente diferenciable \(f:R^{n} \rightarrow R^{m}\).

Teorema del valor medio

Si \(x\) y \(y\) son dos puntos distintos en \(R^{n}\), entonces el segmento de recta \(L(x,y)\) que une \(x\) e \(y\) es

\[ L(x,y) = \left\{ z | z = \theta x + (1 - \theta)y, 0 < \theta < 1 \right\}. \]

Asuma que \(f:R^{n} \rightarrow R\) es continuamente diferenciable en cada punto \(x\) de un conjunto abierto \(S \subset R^{n}\). Sea \(x\) e \(y\) dos puntos de \(S\) tal que el segmento de recta \(L(x,y)\subset S\), entonces existe un punto \(z\) de \(L(x,y)\) tal que

\[ f(y) - f(x) = \left. \frac{\partial f}{\partial x} \right|_{x=z} (y-x). \]

Existencia y unicidad

Una ecuación diferencial de la forma

\[ \dot{x} = f(t,x), \quad x(t_{0}) = x_{0}, \]

podría tener varias soluciones. Por ejemplo, si consideramos la siguiente función

(34)\[ \dot{x} = x^{1/3}, \quad x(0) = 0, \]

si resolvemos la Ec. (34), utilizando Laplace por ejemplo, obtenemos que la siguiente solución

\[ x(t) = \left( \frac{2t}{3} \right)^{3/2}. \]

Podemos observar que esta solución no es única debido a que \(x(t) \equiv 0\) es otra solución.

Theorem 1 (Existencia local y unicidad)

Sea \(f(t,x)\) continuo a pedazos en \(t\) y que satisface la condición de Lipschitz

\[ \| f(t,x) - f(t,y) \| \leq L\|x-y \|, \]

\(\forall x,y \in B = \{x\in R^{n} | \|x-x_{0}\|\leq r\}\), \(\forall t\in[t_{0},t_{1}]\). Entonces, existe algún \(\delta >0\) tal que la ecuación de estado

\[ \dot{x} = f(t,x), \quad \text{con } x(t_{0}) = x_{0}, \]

tiene una solución única sobre \([t_{0},t_{0}+\delta]\).

Ejemplo

• Considere la siguiente función

\[\begin{split} f(x) = \begin{bmatrix} -x_{1} + x_{1}x_{2} \\ x_{2} - x_{1}x_{2} \end{bmatrix}. \end{split}\]

Ejemplo

• Considere la siguiente función

\[\begin{split} f(x) = \begin{bmatrix} x_{2} \\ -\text{sat}(x_{1} + x_{2}) \end{bmatrix}, \end{split}\]

donde la función de saturación está definida por

\[\begin{split} \text{sat}(y) = \left\{ \begin{matrix} -1, & \text{para } y<-1, \\ y, & \text{para } |y|\leq-1, \\ 1, & \text{para } y>1 \end{matrix} \right. \end{split}\]

Ejemplo

• Considere el siguiente sistema escalar

\[ \dot{x} = -x^{2}, \quad x(0) = -1. \]

Lemma 1

[Khalil, 1992] Sea \(f:[a,b]\times D \rightarrow R^{m}\) continua para algún dominio \(D\subset R^{n}\). Suponga que \(\left[\partial f/\partial x \right]\) existe y es continua sobre \([a,b]\times D\). Si, para un subconjunto convexo \(W\subset D\), hay una constante \(L\geq0\) tal que

\[ \left\| \frac{\partial f}{\partial x}(t,x) \right\| \leq L,\]

sobre \([a,b]\times W\), entonces

\[ \left\| f(t,x) - f(t,y) \right\| \leq L\left\| x - y \right\|,\]

para todo \(t\in[a,b],x\in W\) e \(y\in W\).

Lemma 2

[Khalil, 1992] Sea \(f(t,x)\) continua sobre \([a,b]\times D\), para algún dominio \(D\subset R^{n}\). Si \(\left[\partial f/\partial x\right]\) existe y es continua sobre \([a,b]\times D\), entonces \(f\) es localmente Lipschitz en \(x\) sobre \([a,b]\times D\).

Lemma 3

[Khalil, 1992] Sea \(f(t,x)\) continua sobre \([a,b]\times R^{n}\). Si \(\left[\partial f/\partial x\right]\) existe y es continua sobre \([a,b]\times R^{n}\), entonces \(f\) es globalmente Lipschitz en \(x\) sobre \([a,b]\times R^{n}\) si y sólo si \(\left[\partial f/\partial x\right]\) es uniformemente acotado sobre \([a,b]\times R^{n}\).

Theorem 2 (Existencia global y unicidad)

[Khalil, 1992] Suponga que \(f(t,x)\) es continua definida a pedazos sobre \(t\) y satisface

\[\begin{split} \begin{aligned} \|f(t,x) - f(t,y) \| &\leq L\|x-y\|, \\ \|f(t,x_{0})\| &\leq h, \end{aligned} \end{split}\]

\(\forall x,y\in R^{n}\), \(\forall t \in [t_{0},t_{1}]\). Entonces, la ecuación de estado

\[ \dot{x} = f(t,x), \quad x(t_{0}) = x_{0}, \]

tiene una solución única sobre \([t_{0},t_{1}]\).

Ejemplo

• Considere el siguiente sistema lineal

\[ \dot{x} = A(t)x + g(t) = f(t,x), \]

donde \(A(\cdot)\) y \(g(\cdot)\) son funciones continuas definidas a pedazos sobre \(t\).

Ejemplo

• Considere el siguiente sistema escalar

\[ \dot{x} = -x^{3} = f(x). \]

Theorem 3

[Khalil, 1992] Sea \(f(t,x)\) continua a trozos sobre \(t\) y localmente Lipschitz en \(x\) para todo \(t\geq t_{0}\) y toda \(x\) en un dominio \(D\subset R^{n}\). Sea \(W\) un subconjunto compacto de \(D,x_{0}\in W\), suponiendo que cada solución de

\[ \dot{x} = f(t,x), \quad x(t_{0}) = x_{0}, \]

yace enteramente en \(W\). Entonces, hay una solución única que está definida para todo \(t\geq t_{0}\).

Theorem 4

[Khalil, 1992] Sea \(f(t,x)\) continua a pedazos sobre \(t\) y Lipschitz en \(x\) sobre \([t_{0},t_{1}]\times W\) con una constante Lipschitz \(L\), donde \(W\subset R^{n}\) es un conjunton conectado. Sea \(y(t)\) y \(z(t)\) soluciones de

\[ \dot{y} = f(t,y), \quad y(t_{0}) = y_{0}, \]

y

\[ \dot{z} = f(t,z) + g(t,z), \quad z(t_{0}) = z_{0}, \]

tal que \(y(t)\), \(z(t)\in W\) para todo \(t\in[t_{0},t_{1}]\). Suponga que

\[ \|g(t,x)\| \leq \mu,\quad \forall (t,x)\in [t_{0},t_{1}]\times W, \]

para algún \(\mu >0\), y

\[ \|y_{0}-z_{0}\| \leq \gamma, \]

entonces

\[ \|y(t) -z(t)\| \leq \gamma \exp\left[ L(t-t_{0}) \right] + \frac{\mu}{L}\left\{ \exp\left[ L(t-t_{0}) \right] - 1 \right\}, \quad \forall t\in [t_{0},t_{1}]. \]

Theorem 5

[Khalil, 1992] Sea \(f(t,x,\lambda)\) continua en \((t,x,\lambda)\) y localmente Lipschitz en \(x\) (uniformemente en \(t\) y \(\lambda\)) sobre \([t_{0},t_{1}]\times D \times \left\{ \|\lambda - \lambda_{0} \leq c\right\}\) donde \(D\subset R^{n}\) es un conjunto abierto conectado. Sea \(y(t,\lambda_{0})\) una solución de \(\dot{x}=f(t,x,\lambda_{0})\) con \(y(t_{0},\lambda_{0})=y_{0}\in D\). Suponga que \(y(t,\lambda_{0})\) está definida y pertenece a \(D\) para todo \(t\in [t_{0},t_{1}]\). Entonces, dado \(\varepsilon>0\), hay un \(\delta>0\), tal que si

\[ \|z_{0}-y_{0}\| < \delta, \quad \|\lambda-\lambda_{0}\| <\delta, \]

entonces hay una solución única \(z(t,\lambda)\) de \(\dot{x}=f(t,x,\lambda)\) definida sobre \([t_{0},t_{1}]\), con \(z(t_{0},\lambda)=z_{0}\) y \(z(t,\lambda)\) satisface

\[ \|z(t,\lambda) - y(t,\lambda_{0})\| < \varepsilon, \quad \forall t \in [t_{0}, t_{1}]. \]