Observabilidad de sistemas dinámicos

Concepto de observabilidad

Considere un sistema \(n\)-dimensional en representación de espacio-estado como sigue

(54)\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx + Du, \end{aligned} \end{split}\]

donde \(A\), \(B\), \(C\) son matrices de dimensión \(n\times n\), \(n\times 1\), y \(1\times n\), respectivamente. Además, \(D\) es escalar.

Supongamos que queremos estimar el estado de un sistema dinámico a partir de sus entradas \(u\) y salidas \(y\) como se aprecia en la Fig. 15.

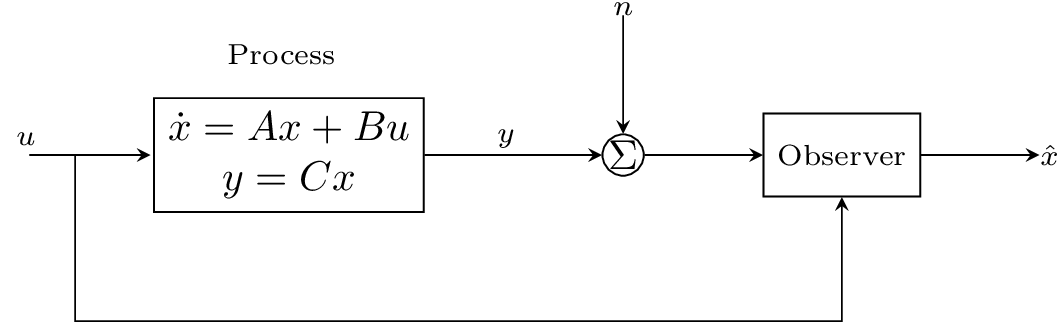
Fig. 15 Diagrama a bloques de un observador de estados. El observador utiliza la señal medida \(y\) y la entrada \(u\) para estimar el proceso denotado como \(\hat{x}\).

Para ello, considere que tenemos sólo una señal medida \(y\) que pueda ser afectada por ruido \(n\). Aquí, denotamos \(\hat{x}\) como el estado estimado dado por el observador.

Definition 7

Un sistema LTI es observable si es posible determinar el estado de un sistema \(x\) a través de las mediciones de \(y\) y \(u\) sobre el intervalo \([0,t]\), para cualquier \(t>0\).

Entonces, definimos la matriz \(n\times n\)

\[\begin{split} V = \begin{bmatrix} C \\ CA \\ \vdots \\ CA^{n-1} \end{bmatrix}, \end{split}\]

entonces el sistema (54) es observable si y sólo si la matriz \(V\) tiene rango \(n\) o bien, \(\text{det}\{V\} \neq 0\).

Note

La controlabilidad es una propiedad de \((A,B)\) mientras que observabilidad es una propiedad de \((A,C)\).

Ejemplo

• Considere la siguiente función de transferencia

\[ G(s) = \frac{N(s)}{D(s)} = \frac{2s-1}{s^{2}-1.5s-1} = \frac{2s-1}{(s-2)\left(s+\frac{1}{2}\right)}, \]

y determine si el sistema es observable.

Ejemplo

• Considere la siguiente función de transferencia

\[ G(s) = \frac{N(s)}{D(s)} = \frac{2s+1}{s^{2}-1.5s-1} = \frac{2s+1}{(s-2)\left(s+\frac{1}{2}\right)}, \]

y determine si el sistema es observable.

Ejemplo

• Considere un modelo de dos compartimientos como se muestra en la Fig. 16

Fig. 16 Modelo compartimental.

Asuma que la concentración del primer compartimiento puede ser medido y que el sistema está descrito por el siguiente sistema lineal

\[\begin{split} \begin{aligned} \dot{c} &= \begin{bmatrix} -k_{0}-k_{1} & k_{1} \\ k_{2} & -k_{2} \end{bmatrix}c + \begin{bmatrix} b_{0} \\ 0 \end{bmatrix}u, \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}x. \end{aligned} \end{split}\]

El primer compartimiento corresponde a la concentración de fármaco en el plasma sanguíneo mientras que el segundo representa la concentración del fármaco en el tejido donde es activo.

Determine si el sistema es observable.

Formas canónicas de observabilidad

Un sistema SISO, está en la forma canónica observable si sus dinámicas están dadas como sigue

\[\begin{split} \begin{aligned} \dot{z} &= \begin{bmatrix} -a_{1} & 1 & 0 & \cdots & 0 \\ -a_{2} & 0 & 1 & \cdots & 0 \\ \vdots & & & \ddots & \\ -a_{n-1} & 0 & 0 & \cdots & 1 \\ -a_{n} & 0 & 0 & \cdots & 0 \end{bmatrix}z + \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n-1} \\ b_{n} \end{bmatrix}u, \\ y &= \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \end{bmatrix}z. \end{aligned} \end{split}\]

Si la entrada \(u\) y la salida \(y\) están disponibles, entonces el estado \(z_{1}\) puede ser estimado.

Estimación de estados

Considere el siguiente sistema \(n\)-dimensional en representación de espacio-estado

(55)\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx. \end{aligned} \end{split}\]

Una estimación de los estados del sistema se puede obtener simulando las ecuaciones (55) dada una entrada adecuada. Por lo tanto, el estimador de estados está dado por la siguiente expresión

\[ \dot{\hat{x}} = A\hat{x} + Bu. \]

Para determinar las propiedades de esta estimación, es necesario definir el error de estimación \(\tilde{x} := x - \hat{x}\), de modo que el sistema se reescribe como sigue

\[ \dot{\tilde{x}} = A \tilde{x}. \]

Note

Si todos los eigenvalores de la matriz \(A\) se encuentran en el semi plano izquierdo, entonces el error \(\tilde{x}\rightarrow 0\).

Considere el siguiente observador

(56)\[ \dot{\hat{x}} = A\hat{x} + Bu + L(y-C\hat{x}). \]

Podemos observar que la retroalimentación de la salida se logra agregando el término \(L(y-C\hat{x})\) la cual es proporcional a la diferencia entre la salida observada y la salida estimada por el sistema (56). Por lo tanto

\[ \dot{\hat{x}} = (A - LC)\hat{x}. \]

Si la matriz \(L\) se escoge de manera que la matriz \(A-LC\) tiene eigenvalores con parte real negativa, entonces el error \(\tilde{x}\rightarrow 0\).

Note

La tasa de convergencia está determinada por una adecuada selección de los eigenvalores.

Diseño de observador via asignación de eigenvalores

Theorem 10

Considere el siguiente sistema SISO

(57)\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx. \end{aligned} \end{split}\]

Sea \(\lambda_{A}(s) = s^{n} + a_{1}s^{n-1} + \cdots + a_{n-1}s + a_{n}\) el polinomio característico para \(A\). Si el sistema es observable, entonces el sistema dinámico

(58)\[ \dot{\hat{x}} = A\hat{x} + Bu + L(y - C\hat{x}), \]

es un observador para el sistema, con \(L\) elegida como sigue

\[\begin{split} L = V^{-1}\tilde{V} \begin{bmatrix} p_{1} - a_{1} \\ p_{2} - a_{2} \\ \vdots \\ p_{n} - a_{n} \\ \end{bmatrix}, \end{split}\]

donde las matrices \(V\) y \(\tilde{V}\) están dadas por

\[\begin{split} V = \begin{bmatrix} C \\ CA \\ \vdots \\ CA^{n-1} \end{bmatrix}, \quad \tilde{V} = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 \\ a_{1} & 1 & 0 & \cdots & 0 & 0 \\ a_{2} & a_{1} & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n-2} & a_{n-3} & a_{n-4} & \cdots & 1 & 0 \\ a_{n-1} & a_{n-2} & a_{n-3} & \cdots & a_{1} & 1 \\ \end{bmatrix}. \end{split}\]

El error del observador \(\tilde{x} = x - \hat{x}\) está dado por una ecuación diferencial que tiene como polinomio característico

\[ p(s) = s^{n} + p_{1}s^{n-1} + \cdots + p_{n}. \]

El sistema dado en la Ec. (58) es llamado observador de estados del sistema (57) y su diagrama a bloques se muestra en la Fig. 17.

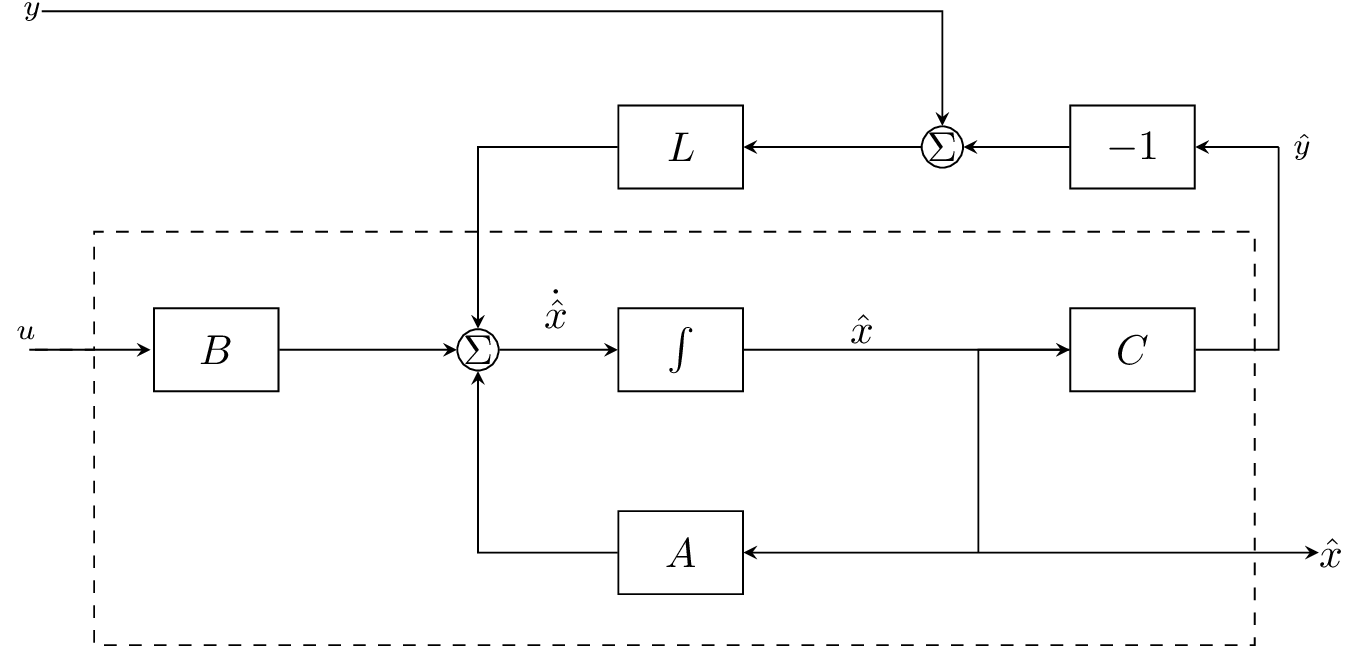
Fig. 17 Diagrama a bloques del observador de estados. Para producir una estimación \(\hat{x}\) se consideran las entradas \(u\) e \(y\) como entradas y \(L\) como la ganancia del observador.

Ejemplo

• Considere un modelo de dos compartimientos como se muestra en la Fig. 16

\[\begin{split} \begin{aligned} \dot{c} &= \begin{bmatrix} -k_{0}-k_{1} & k_{1} \\ k_{2} & -k_{2} \end{bmatrix}c + \begin{bmatrix} b_{0} \\ 0 \end{bmatrix}u, \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}x, \end{aligned} \end{split}\]

y diseñe un observador de estados.

Cálculo de la ganancia del observador

Ejemplo

• Considere el siguiente modelo lineal que representa la dirección de un vehículo, considerando la desviación de trayectoria lateral \(y\) con el ángulo de dirección \(u\)

\[\begin{split} \begin{aligned} \dot{x} &= \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}x + \begin{bmatrix} \gamma \\ 1 \end{bmatrix}u, \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}x. \end{aligned} \end{split}\]

Diseñe un observador de estados y calcule su ganancia.

Note

El estado \(x_{1}\) representa la desviación de la trayectoria lateral y \(x_{2}\) la velocidad de giro.

Ejemplo

• Considere el siguiente modelo SISO en representación de espacio de estados

\[\begin{split} A = \begin{bmatrix} -1 & -0.75 \\ 1 & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 1 \end{bmatrix} \end{split}\]

Teorema de dualidad

Sea el sistema \(\Sigma_{1}\) representado por las siguientes ecuaciones

\[\begin{split} \Sigma_{1} := \left\{ \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx, \end{aligned} \right. \end{split}\]

y el sistema dual \(\Sigma_{2}\) definido como

\[\begin{split} \Sigma_{2} := \left\{ \begin{aligned} \dot{z} &= A^{*}z + C^{*}v, \\ n &= B^{*}z, \end{aligned} \right. \end{split}\]

donde \(z\) es el vector de estado, \(v\) el vector de control, \(n\) el vector de salida y \({}^{*}\) denota la transpuesta conjugada.

El teorema de dualidad menciona que el sistema \(\Sigma_{1}\) es completamente controlable (observable) si y sólo si el sistema \(\Sigma_{2}\) es completamente observable (controlable).

Condiciones necesarias

Para el sistema \(\Sigma_{1}\)

• Condición de controlabilidad

\[ \text{rank}\left\{ \begin{bmatrix} B & AB & \cdots & A^{n-1}B \end{bmatrix} \right\} = n. \]

• Condición de observabilidad

\[ \text{rank}\left\{ \begin{bmatrix} C^{*} & A^{*}C^{*} & \cdots & (A^{*})^{n-1}C^{*} \end{bmatrix} \right\} = n. \]

Para el sistema \(\Sigma_{2}\)

• Condición de controlabilidad

\[ \text{rank}\left\{ \begin{bmatrix} C^{*} & A^{*}C^{*} & \cdots & (A^{*})^{n-1}C^{*} \end{bmatrix} \right\} = n. \]

• Condición de observabilidad

\[ \text{rank}\left\{ \begin{bmatrix} B & AB & \cdots & A^{n-1}B \end{bmatrix} \right\} = n. \]

Procedimiento para obtener la ganancia del observador via Lyapunov

La ganancia \(L\) del observador de estados \eqref{eqn:observer}, se pude obtener a partir de la siguiente expresión [Coronel-Escamilla et al., 2017]

\[ L = S^{-1}C^{T}, \]

donde \(S\) es la solución única de la ecuación algebráica de Lyapunov

(59)\[ -\lambda S - A^{T}S - SA + C^{T}C = 0, \]

donde \(\lambda\) denota el parámetro para sintonizar la convergencia del observador (56).

El siguiente fragmento de código permite encontrar la solución a la Ec. (59)

def lyapunov(lamb,N):
    S = np.zeros((N,N))

    for k in range(1,N+1):
        for l in range(1,N+1):
            c = nchoosek(l+k-2,k-1)
            S[l-1][k-1] = ((-1)**(l+k)*c)/lamb**(l+k-1)

    return S

donde la función nchoosek está dada como sigue

\[ {}_{n}C_{k} = \binom{n}{k} = \frac{n!}{(n-k)!k!}, \]

y su representación en Python como

def nchoosek(n, k):
    return int(factorial(n)/(factorial(k)*factorial(n-k)))

Control utilizando estimadores de estado

Considere un sistema en representación de espacio de estados de la forma

\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx. \end{aligned} \end{split}\]

Este sistema sólo tiene una salida disponible y es necesario diseñar un control por retroalimentación. Para ello, asumimos que el sistema es controlable así como observable y que además, \(u\) e \(y\) son escalares.

Considerando la siguiente ley de control (retroalimentación), tenemos

\[ u = -Kx + k_{r}r. \]

Bajo la suposición de que todos los estados son medibles, proponemos el diseño de un observador para estimar el estado \(\hat{x}\) a partir de las entradas y las salidas.

Si todos los estados no están disponibles o bien, no son medibles, entonces proponemos la siguiente ley de control

\[ u = -K\hat{x}+k_{r}r, \]

donde \(\hat{x}\) es la salida del observador de estados

\[ \dot{\hat{x}} = A\hat{x} + Bu + L(y - C\hat{x}). \]

Para analizar el sistema en lazo cerrado, definimos la siguiente variable

\[ \tilde{x}:=x-\hat{x}, \]

y la reemplazamos en la variable de estado \(\hat{x}\). Con esto obtenemos la siguiente expresión

\[ \dot{x} = (A-BK)x + BK\tilde{x}+Bk_{r}r, \]

o en representación de espacio de estados como sigue

\[\begin{split} \begin{bmatrix} \dot{x} \\ \dot{\tilde{x}} \end{bmatrix} = \begin{bmatrix} A - BK & BK \\ 0 & A-LC \end{bmatrix} \begin{bmatrix} x \\ \tilde{x} \end{bmatrix} + \begin{bmatrix} Bk_{r} \\ 0 \end{bmatrix}r. \end{split}\]

Por consiguiente, el polinomio característico del sistema está dado por la siguiente ecuación

\[ \phi(\lambda) = \left| \lambda I - A + BK \right| \left| \lambda I - A + LC \right| \]

Un diagrama de un sistema de control basado en observador se presenta en la Fig. 18.

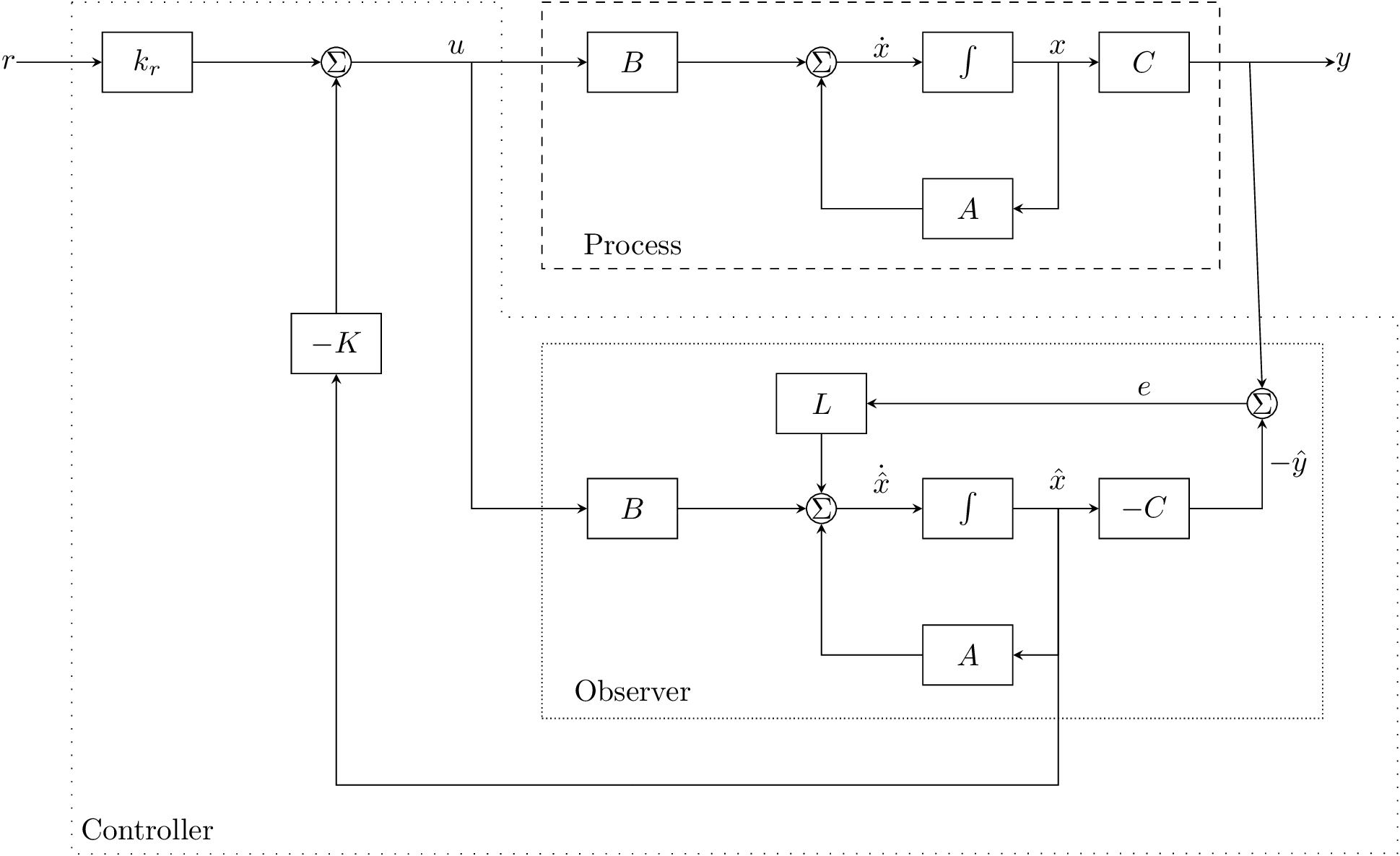
Fig. 18 Diagrama a bloques de un sistema de control basado en observador. El observador utiliza la salida estimada \(y\) y la entrada \(u\) para obtener una aproximación de los estados \(x\). Esta estimación se utiliza por un sistema de control por retroalimentación de estados para corregir la entrada.