Modelado con ecuaciones diferenciales de primer orden

Crecimiento y decaimiento

La siguiente ED sirve para modelar fenómenos de crecimiento o decaimiento

(51)\[ \frac{\mathrm{d}x}{\mathrm{d}t} = kx, \quad x\left( t_{0} \right) = x_{0}, \]

donde \(k\) es una constante de proporcionalidad.

Atención

En áreas como la física y la química, la Ec. (51) es conocida como reacción de primer orden.

Crecimiento de bacterias

En un cultivo de bacterias, el número inicial se denota por \(P_{0}\). Después de 1h, es decir en \(t=1\), el número de bacterias es \(\frac{3}{2}P_{0}\). Si la razón de crecimiento es proporcional al número de bacterias \(P(t)\), entonces podemos ocupar la Ec. (51) para modelar este problema. Haciendo el cambio de la variable \(x\) por \(P\), se tiene

(52)\[ \frac{\mathrm{d}P}{\mathrm{d}t} - kP = 0. \]

Como se puede observar, el modelo (52) es lineal y se encuentra en la forma estándar. Por lo tanto, podemos utilizar el método de variables separables para resolverlo. Entonces

\[ e^{-\int k~\mathrm{d}t} = e^{-kt}. \]

Multiplicando por ambos lados de la Ec. (52)

\[\begin{split} \begin{aligned} e^{-kt} \frac{\mathrm{d}P}{\mathrm{d}t} - e^{-kt}kP &= 0, \\ \frac{\mathrm{d}}{\mathrm{d}t} \left[ e^{-kt}P \right] &= 0. \end{aligned} \end{split}\]

Integrando por ambos lados

\[\begin{split} \begin{aligned} e^{-kt}P &= c, \\ P &= ce^{kt}. \end{aligned} \end{split}\]

Tomando en cuenta la condición inicial \(P(0) = P_{0}\), se tiene

\[\begin{split} \begin{aligned} P_{0} &= ce^{0}, \\ P_{0} &= c. \end{aligned} \end{split}\]

Por consiguiente

\[ P = P_{0}e^{kt}. \]

En \(t=1\), se tiene que

\[\begin{split} \begin{aligned} \frac{3}{2}P_{0} &= P_{0}e^{k}, \\ \frac{3}{2} &= e^{k}. \end{aligned} \end{split}\]

Despejando \(k\), se obtiene

\[ \begin{aligned} k &= \ln\left(\frac{3}{2}\right), &= 0.4055, \end{aligned} \]

y por tanto

\[ P = P_{0}e^{0.4055t}. \]

Vida media del plutonio

Un reactor convierte uranio 238 en isótopo plutonio 239. Después de 15 años, se ha demostrado que 0.043% de la cantidad inicial \(A_{0}\) de plutonio se ha desintegrado. Si la razón de desintegración es proporcional a la cantidad que queda, determine la vida media de ese isótopo.

Ley de Newton de enfriamiento o calentamiento

La ley empírica de Newton de enfriamiento o calentamiento de un objeto se expresa con la siguiente ecuación diferencial de primer orden

(53)\[ \frac{\mathrm{d}T}{\mathrm{d}t} - k \left(T - T_{m}\right), \]

donde \(k\) representa la constante de proporcionalidad, \(T(t), ~t>0\) la temperatura del objeto, \(T_{m}\) la temperatura del medio que rodea al objeto.

Enfriamiento de un pastel

La temperatura de un pastel al salir del horno es de 149° C. Tres minutos después es de 93° C. ¿Cuánto tiempo de tomó al pastel enfriarse hasta la temperatura ambiente de 21° C?

De la Ec. (53) tenemos que $T_{m} = 21. Por lo tanto, el PVI se plantea de la siguiente forma

(54)\[ \frac{\mathrm{d}T}{\mathrm{d}t} - k \left(T - 21\right), \quad T(0) = 149. \]

Como se puede observar, la (54) es lineal y se puede resolver utilizando variables separables. Entonces, se tiend

\[ \frac{\mathrm{d}T}{T - 21} = k~\mathrm{d}t. \]

Integrando por ambos lados de la igualdad

\[\begin{split} \begin{aligned} \ln\left(T - 21 \right) &= kt + c, \\ T - 21 &= e^{kt + c}, \\ T &= e^{kt}e^{c} + 21, \\ &= c_{1}e^{kt} + 21 \end{aligned} \end{split}\]

donde \(c_{1} := e^{c}\).

Tomando la condición inicial para encontrar el valor de \(c_{1}\)

\[\begin{split} \begin{aligned} 149 &= c_{1}e^{0} + 21, \\ 149 - 21 &= c_{1}, \\ 128 &= c_{1}. \end{aligned} \end{split}\]

Por consiguiente

\[ T = 128e^{kt} + 21. \]

Dado que \(T(3) = 200\), entonces

\[\begin{split} \begin{aligned} 93 &= 128e^{3k} + 21, \\ 72 &= 128e^{3k}, \\ \frac{72}{128} &= e^{3k}. \end{aligned} \end{split}\]

Finalmente, si despejamos \(k\) obtenemos

\[\begin{split} \begin{aligned} \ln\left(e^{3k} \right) &= \ln\left(\frac{72}{128} \right), \\ 3k &= \ln\left(\frac{72}{128} \right), \\ k &= \frac{-0.5754}{3}, \\ &= -0.1918. \end{aligned} \end{split}\]

\[ T = 128e^{-0.1918t} + 21. \]

Circuitos en serie

La relación que establece el flujo electromagnético \(\phi\) y la corriente \(i\) que lo produce está dada por la siguiente ecuación

\[ \phi = L i, \]

donde \(L\) es una constante que depende de los factores geométricos y de entorno llamada inductancia.

Los cambios de flujo electromagnético originan potenciales eléctricos relacionados por la Ley de Faraday

\[ u_{L} = - \dot{\phi}, \]

donde \(u_{L}\) denota el voltaje en las terminales de la inductancia a razón del cambio de flujo. Por consiguiente, la Ley de Faraday se puede expresar como sigue

\[ u_{L} = - L \dot{\phi}. \]

En elementos resistivos el voltaje \(u_{R}\) entre el componente y la corriente \(i\) que circula por él obedecen a la Ley de Ohm dada como siguiente

(55)\[ u_{R} = Ri, \]

donde \(R\) es una constante que depende del componente denominado resistencia.

El voltaje \(u_{C}\) entre las terminales de una capacitancia y la carga \(q\) siguen la siguiente relación

\[ u_{C} = \frac{Q}{C} \equiv \frac{1}{C} \int i \mathrm{d}t, \]

donde \(C\) es una constante que depende de la geometría y el entorno denominada capacitancia. Si consideramos que la corriente se define como una variación temporal de carga

\[ i = \dot{Q}, \quad Q = \int i \mathrm{d}t, \]

entonces \(u_{C}\) se expresa en los siguientes términos

(56)\[ u_{C} = \frac{1}{C} \int i\mathrm{d}t. \]

Considere el circuito mostrado en la Figura 2

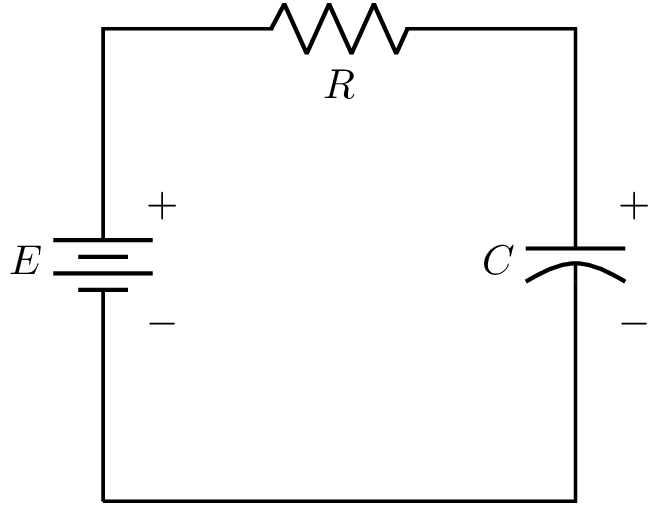
Figura 2 Modelo de circuito R-C.

Aplicando la Ley de tensiones de Kirchhoff, obtenemos

(57)\[ u_{R} + u_{C} = E. \]

Sustituyendo (55) y (56) en (57), tenemos

\[ Ri + \frac{1}{C} \int i \mathrm{d}t = E, \]

expresado la ecuación anterior en términos de la carga \(Q\), tenemos la siguiente expresión

(58)\[ R \dot{Q} + \frac{1}{C}Q = E, \]

Aplicando la Ley de corrientes de Kirchhoff, obtenemos

\[ i_{R} + i_{C} = i, \]

dado que el voltaje entre los componentes eléctricos es el mismo y lo denotamos por \(u\), tenemos

\[ \frac{u}{R} + C \dot{u} = i. \]

Considerando el modelo dado en la Ec. (58) y tomando \(V\) como la carga en el capacitor dividida por la capacitancia \(V := \frac{Q}{C}\) y \(\dot{V}:= \frac{\dot{Q}}{C}\), sustituyendo tenemos

\[\begin{split} \begin{aligned} R\dot{V}C + \frac{1}{C}VC &= E, \\ R\dot{V}C + V &= E. \end{aligned} \end{split}\]

Entonces, el modelo del circuito RC mostrado en la Figura 2 está dado por la siguiente ecuación

\[ \dot{V} + \frac{1}{RC}V = \frac{1}{RC} E. \]