Sistemas de ecuaciones diferenciales lineales

Resortes acoplados

Dos masas \(m_{1}\) y \(m_{2}\) se encuentran conectadas a dos resortes \(A\) y \(B\) de masa despreciable con constantes de resorte \(k_{1}\), \(k_{2}\). Si \(x_{1}(t)\) y \(x_{2}(t)\) representan los desplazamientos verticales de las masas desde sus posiciones de equilibrio podemos representar la elongación neta del resorte \(B\) por la expresión \(x_{2} - x_{1}\).

A partir de la ley de Hooke tenemos que los resortes \(A\) y \(B\) ejercen fuerzas \(-k_{1}x_{1}\) y \(k_{2}\left(x_{2} - x_{1} \right)\) en \(m_{1}\). Ante la ausencia de fuerzas externa y amortiguamiento, la fuerza neta en la masa \(m_{1}\) está representada por \(-k_{1}x_{1} + k_{2}\left(x_{2} - x_{1} \right)\). Por la segunda ley de Newton se tiene

\[ m_{1}\frac{\mathrm{d}^{2}x_{1}}{\mathrm{d}t^{2}} = -k_{1}x_{1} + k_{2}\left(x_{2} - x_{1} \right). \]

Para el caso de la masa \(m_{2}\) sólo se ve afectada por la elongación neta de \(B\), esto es \(-k_{2}\left( x_{2} - x_{1} \right)\). Por tanto se obtiene

\[ m_{2}\frac{\mathrm{d}^{2}x_{2}}{\mathrm{d}t^{2}} = -k_{2}\left(x_{2} - x_{1} \right). \]

Entonces, el sistema de ecuaciones diferenciales de segundo orden que describen el movimiento del sistema acoplado está dado por

\[\begin{split} \begin{aligned} m_{1}x''_{1} &= -k_{1}x_{1} + k_{2}\left(x_{2} - x_{1} \right), \\ m_{2}x''_{2} &= -k_{2}\left(x_{2} - x_{1} \right). \end{aligned} \end{split}\]

Ejemplo

Considere las siguientes masas \(m_{1} = m_{2} = 1\), y constantes de resorte \(k_{1}=6\), \(k_{2} = 4\). Resuelva el sistema de ecuaciones considerando las condiciones iniciales \(x_{1}(0)=0\), \(x'_{1}(0)=1\), \(x_{2}(0)=0\), \(x'_{2}(0)=-1\).

Red eléctrica

Las corrientes \(i_{1}(t)\) e \(i_{2}(t)\) de una red que contiene un inductor, un resistor y un capacitor están gobernadas por el siguiente sistema de ecuaciones diferenciales de primer orden

\[\begin{split} \begin{aligned} L \frac{\mathrm{d}i_{1}}{\mathrm{d}t} + Ri_{2} &= E(t), \\ RC \frac{\mathrm{d}i_{2}}{\mathrm{d}t} + i_{2} - i_{1} &= 0. \end{aligned} \end{split}\]

Considere las siguientes condiciones \(E(t) = 60\) V, \(L=1\) h, \(R=50~\Omega\), \(C=10^{-4}\) f. Además, tome en cuenta que al inicio las corrientes \(i_{1} = i_{2} = 0\).

Péndulo simple

Considere el péndulo simple mostrado en la siguiente

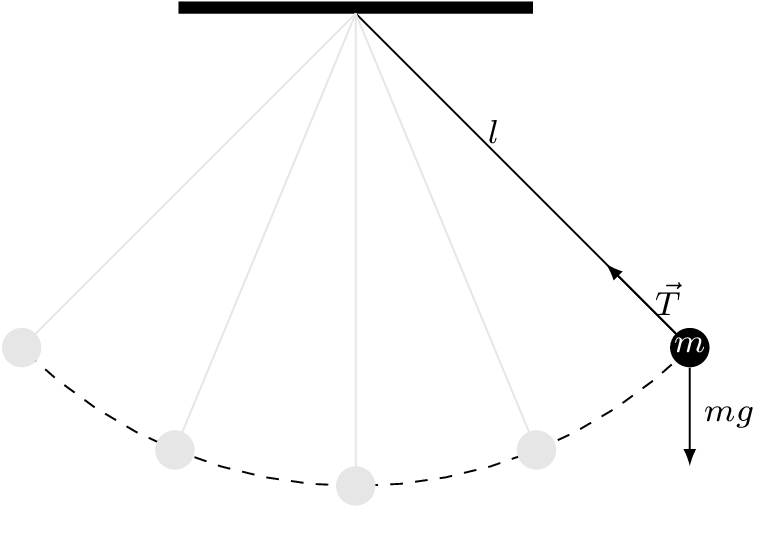
Figura 3 Diagrama de péndulo simple sin fuerza externa.

donde \(l\) denota la longitud de la varilla, y \(m\) la masa de la bola.

Cuya representación en espacio de estados está dada como sigue

(64)\[\begin{split} \begin{aligned} \dot{x_{1}} &= x_{2}, \\ \dot{x_{2}} &= -\frac{g}{l}\sin(x_{1}) - \frac{k}{m}x_{2}. \end{aligned} \end{split}\]