Función de transferencia

Función de transferencia#

Considere un sistema lineal invariante en el tiempo (LTI) cuya función de transferencia es \(G(s)\) y la entrada así como la salida se representan por \(x(t)\), \(y(t)\), respectivamente. Dicha función se puede escribir como el cociente de dos polinomios en \(s\), esto es

\[ G(s) = \frac{p(s)}{q(s)} = \frac{p(s)}{(s+s_{1})(s+s_{2})\cdots(s+s_{n})}, \]

o bien

\[ G(s) = \frac{b_{n}s^{n} + \cdots + b_{3}s^{3} + b_{2}s^{2} + b_{1}s + b_{0}}{a_{n}s^{n} + \cdots + a_{3}s^{3} + a_{2}s^{2} + a_{1}s + a_{0}}. \]

La transformada de Laplace de la salida \(Y(s)\) es

\[ Y(s) = G(s)X(s) = \frac{p(s)}{q(s)}X(s), \]

donde \(X(s)\) es la transformada de Laplace de la entrada \(x(t)\).

La respuesta en estado estacionario de un sistema estable LTI a una entrada sinusoidal no depende de las condiciones iniciales. Considerando que \(Y(s)\) tiene únicamente polos distintos (simples), la ecuación anterior se puede representar en fracciones parciales como sigue

\[ Y(s) = G(s)X(s) = G(s) \frac{\omega X}{s^{2} + \omega^{2}}, \]
(3)#\[ Y(s) = \frac{a}{s + j\omega} + \frac{\bar{a}}{s - j\omega} + \frac{b_{1}}{s + s_{1}} + \frac{b_{2}}{s + s_{2}} + \dots + \frac{b_{n}}{s + s_{n}}, \]

donde \(a\) y \(b_{i},i=1,2,\dots,n\) son constantes y \(\bar{a}\) es el complejo conjugado de \(a\).

Por consiguiente, si aplicamos la transformada inversa de Laplace a la Ec. (3) tenemos

\[ y(t) = ae^{-j\omega t} + \bar{a}e^{j\omega t} + b_{1}e^{-s_{1} t} + b_{2}e^{-s_{2} t} + \cdots + b_{n}e^{-s_{n} t}, \quad t\geq 0. \]

Función de transferencia propia#

Considere la siguiente función de transferencia

\[ G(s) = \frac{N(s)}{D(s)}, \]

donde \(N(s)\) y \(D(s)\) son dos polinomios con coeficientes reales, entonces tenemos

  • Función impropia. El \(\text{deg }N(s) > \text{deg }D(s)\).

  • Función propia. El \(\text{deg }N(s) \leq \text{deg }D(s)\).

  • Función estrictamente propia. El \(\text{deg }N(s) < \text{deg }D(s)\).

  • Función bipropia. El \(\text{deg }N(s) = \text{deg }D(s)\).

Polos y zeros#

Considere una función de transferencia racional propia

\[ G(s)=\frac{N(s)}{D(s)}, \]

donde \(N(s)\) y \(D(s)\) son polinomios con coeficientes reales y \(\text{deg }N(s) \leq \text{deg }D(s)\).

Definition 18

Un número complejo o real finito \(\lambda\) es un polo de \(G(s)\) si \(|G(s)| = \infty\), donde \(|\cdot|\) denota el valor absoluto. Por otro lado, si \(G(\lambda)=0\) entonces es un zero de \(G(s)\).

Ejemplo

Considere la siguiente función de transferencia

\[ G(s) = \frac{N(s)}{D(s)} = \frac{2\left( s^{3} + 3s^{2} - s - 3 \right)}{\left( s - 1 \right)\left( s + 2 \right)\left(s + 1 \right)^{3}}, \]

obtenga sus polos y zeros.

Ejemplo

Sea \(u(t)=1\) con \(t\leq 0\) la respuesta de escalón unitario, calcule la respuesta de estado cero de la siguiente función de transferencia

\[ Y(s) = G(s)U(s) = \frac{3s-1}{(s+1)(s+2)}\cdot U(s). \]

Estabilidad de sistemas#

  • Sistema absolutamente estable. Todos los polos del sistema estén estrictamente en el semi-plano izquierdo, sin importar la multiplicidad.

  • Sistema marginalmente estable. Al menos un polo está sobre el eje imaginario con multiplicidad uno y el resto están estrictamente en el semi-plano izquierdo, sin importar la multiplicidad.

  • Sistema inestable. Al menos un polo está sobre el eje imaginario con multiplicidad mayor a uno o en el semiplano derecho.

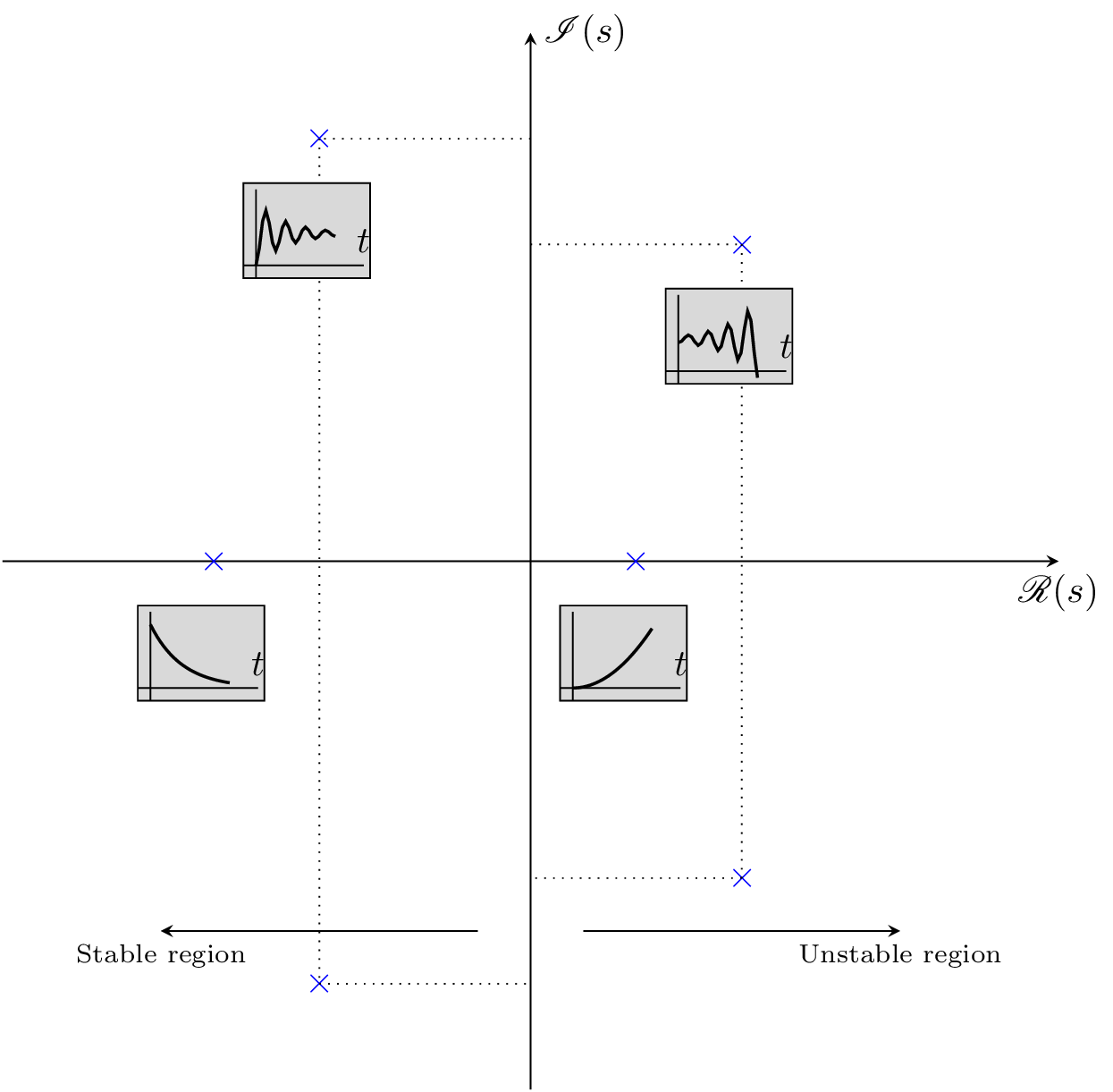
../_images/pzmap_example.png

Figura 1 Mapa de polos y zeros.#

Contenido