Respuesta de estado estacionario

Considere un sistema entrada-salida lineal como se muestra en la siguiente expresión

\[\begin{split} \begin{aligned} \dot{x} &= Ax + Bu, \\ y &= Cx, \end{aligned} \end{split}\]

donde su solución se puede obtener a partir de la ecuación de convolución

(53)\[ y(t) = Ce^{At}x_{0} + \int_{0}^{t}Ce^{A(t-\tau)}Bu(\tau) \mathrm{d}\tau. \]

Como se puede observar, la respuesta del sistema depende de una condición inicial \(x_{0}\) y una entrada \(u\). Además, es posible observar que en esta expresión existen dos componentes: la respuesta transitoria y la respuesta de estado estable. La primera ocurre cuando se aplica una entrada y se observa un desajuste entre la condición inicial y la solución de estado estable. La segunda refleja el comportamiento del sistema bajo las entradas dadas. En la Figura 16 podemos ver estos dos componentes en respuesta ante una entrada de tipo escalón unitario.

Nota

En la práctica, se espera que si la entrada es periódica la respuesta también lo sea. Lo mismo con entradas constantes.

Un escalón unitario, entrada escalón o escalón de Heaviside es una función definida a pedazos como sigue

(54)\[\begin{split} u(t) = \left\{ \begin{matrix} 0, & t = 0, \\ 1, & t>0. \end{matrix} \right. \end{split}\]

Definimos entonces como respuesta escalonada a la salida \(y(t)\) a partir de una condición inicial en el punto de equilibrio del sistema y una entrada \(u(t)\) de la forma (54).

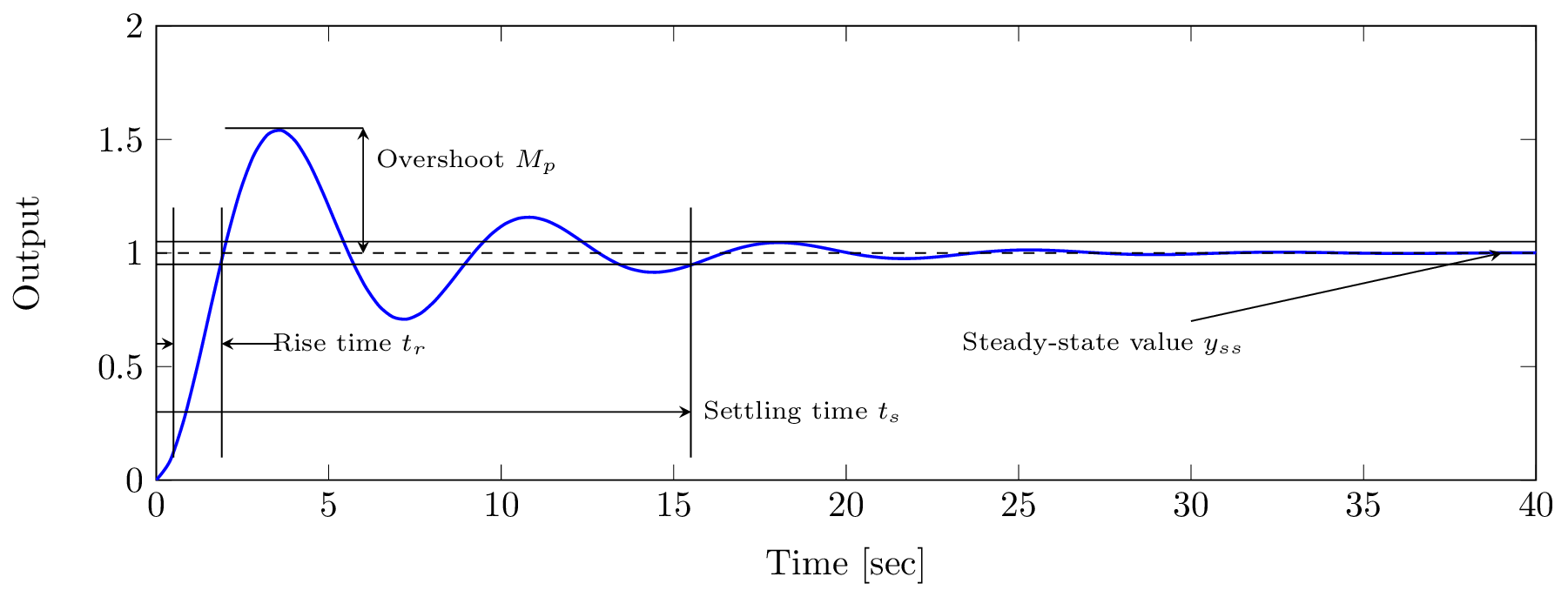
Figura 16 Respuesta del sistema ante una entrada tipo escalón. Se observa el tiempo de subida (Rise time), sobretiro (Overshoot), tiempo de asentamiento (Settling time) y valor en estado estable (Steady-state value).

Utilizando la ecuación de convolución \eqref{eqn:conv_eq}, podemos calcular la respuesta ante una entrada tipo escalón considerando \(x_{0}=0\). Entonces, tenemos

\[\begin{split} \begin{aligned} y(t) &= \int_{0}^{t}Ce^{A(t-\tau)}Bu(\tau)\mathrm{d}\tau = C\int_{0}^{t}e^{A(t-\tau)}B\mathrm{d}\tau, \\ &= C\int_{0}^{t}e^{A\sigma}B\mathrm{d}\sigma = C\left.\left(A^{-1}e^{A\sigma}B \right)\right|^{\sigma = t}_{\sigma=0}, \\ &= CA^{-1}e^{At}B - CA^{-1}B, \end{aligned} \end{split}\]

o bien

\[ y(t) = \underbrace{CA^{-1}e^{At}B}_{\text{transitorio}} \underbrace{- CA^{-1}B}_{\text{estado estable}} \]

Velocidad de respuesta

Definimos como rendimiento transitorio a la velocidad de respuesta o la velocidad en la que el sistema alcanza al estado estable. Generalmente se especifica en términos de tiempo de levantamiento (rise time), tiempo de asentamiento (settling time) y sobretiro (overshoot). El tiempo de levantamiento lo definimos como el tiempo requerido para la respuesta pase de 0 al 90% del valor en estado estacionario como se muestra en la Figura 16. En otras palabras, buscamos el valor más pequeño \(t_{r}\) tal que

\[ y\left(t_{r}\right) = 0.9y_{ss} \]

donde \(t_{s}\) denota el \myindex{tiempo de asentamiento}. Es decir, el tiempo que le toma a la respuesta del sistema alcanzar y mantenerse dentro del \(\pm 2\%\) de su valor en estado estable, o bien, el valor más pequeño \(t_{s}\) tal que

\[ \left|y - y_{ss} \right| \leq 0.02y_{ss}, \quad \forall~ t\geq t_{ss}. \]

Sea \(y_{\max}\) el valor máximo de \(\left|y(t) \right|,~\forall t\geq 0\) o bien

\[ y_{\max} := \max\left| y(t) \right|, \]

entonces el sobretiro se define como sigue

\[ M_{p} := \frac{y_{\max} - y_{ss}}{y_{ss}} \times 100\%. \]