Modelado de sistemas hidráulicos y térmicos

Nivel de líquido de un tanque

Considere el sistema mostrado en la Figura 12 cuyo objetivo es modelar el nivel del agua. Si aplicamos la ley de Torricelli que establece que la rapidez \(v\) de salida del agua a través de un orificio en el fondo de un tanque de altura \(h\) es igual a la velocidad de un cuerpo cayendo libremente desde una altura \(h\) se obtiene la siguiente expresión

(39)\[ v = \sqrt{2gh}, \]

donde \(g\) es la aceleración de la gravedad.

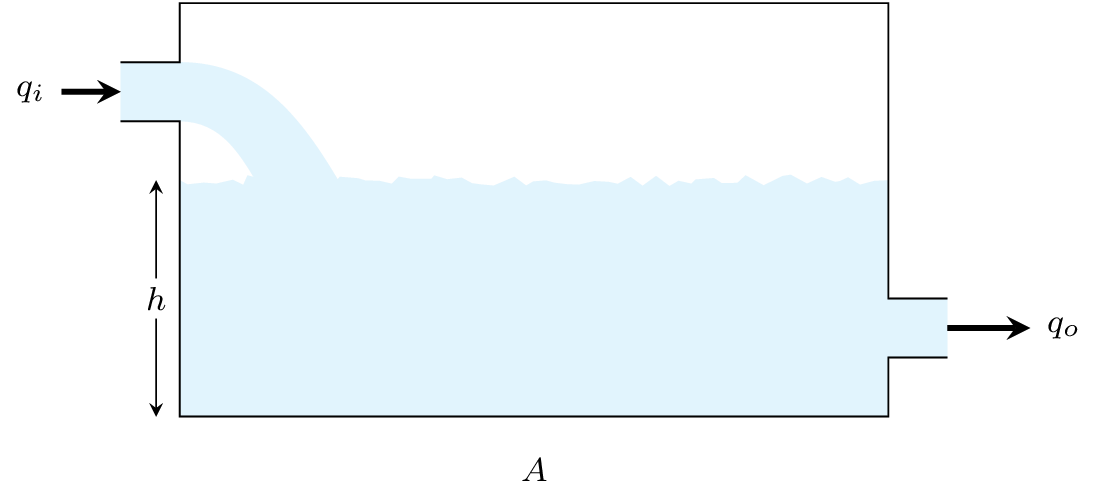
Figura 12 Modelo de un tanque.

El flujo de salida del tanque \(q_{o}\) considerando una sección transversal \(S\), está definido por la siguiente relación

(40)\[ q_{o} = Sv. \]

Sustituyendo (39) en (40) se tiene

(41)\[ q_{o} = S \sqrt{2gh}. \]

Sabemos que el nivel del líquido dentro de un tanque de área \(A\) se puede describir como la diferencia entre el flujo de entrada \(q_{i}\) y el flujo de salida \(q_{o}\) como sigue

(42)\[ A \frac{\mathrm{d}~h}{\mathrm{d}t} = q_{i} - q_{o}. \]

Sustituyendo (41) en (42) obtenemos

\[ A \frac{\mathrm{d}~h}{\mathrm{d}t} = q_{i} - S \sqrt{2gh}, \]

o bien

\[ \frac{\mathrm{d}~h}{\mathrm{d}t} = \frac{q_{i}}{A} - \frac{k}{A} \sqrt{h}, \]

donde \(k:= S \sqrt{2g}\).

Como se puede observar, el modelo que describe el nivel \(h\) de un líquido en un tanque de área \(A\) es no lineal. No obstante, podemos obtener una representación lineal si encontramos el punto de equilibrio tal que \(q_{i} = q_{o}\) y linealizamos el sistema.

Nivel de líquido de dos tanques en cascada

Para obtener un sistema que permita describir el nivel de líquido en dos tanques como se muestra en la , podemos seguir el procedimiento anterior. Donde el flujo de entrada del segundo tanque, es el flujo de salida del primero. Entonces, obtenemos el siguiente sistema de ecuaciones

\[ A_{1} \frac{\mathrm{d}~h_{1}}{\mathrm{d}t} = q_{i} - q_{m}, \]

\[ A_{2} \frac{\mathrm{d}~h_{2}}{\mathrm{d}t} = q_{m} - q_{o}. \]

Sabiendo que

\[ q_{m} := k_{1} \sqrt{h_{1}}, \]

\[ q_{o} := k_{2} \sqrt{h_{2}}. \]

Sustituyendo tenemos

\[ A_{1} \frac{\mathrm{d}~h_{1}}{\mathrm{d}t} = q_{i} - k_{1} \sqrt{h_{1}}, \]

\[ A_{2} \frac{\mathrm{d}~h_{2}}{\mathrm{d}t} = k_{1} \sqrt{h_{1}} - k_{2} \sqrt{h_{2}}, \]

o bien

\[ \frac{\mathrm{d}~h_{1}}{\mathrm{d}t} = \frac{q_{i}}{A_{1} } - \frac{k_{1}}{A_{1} } \sqrt{h_{1}}, \]

\[ \frac{\mathrm{d}~h_{2}}{\mathrm{d}t} = \frac{k_{1}}{A_{2}} \sqrt{h_{1}} - \frac{k_{2}}{A_{2}} \sqrt{h_{2}}. \]

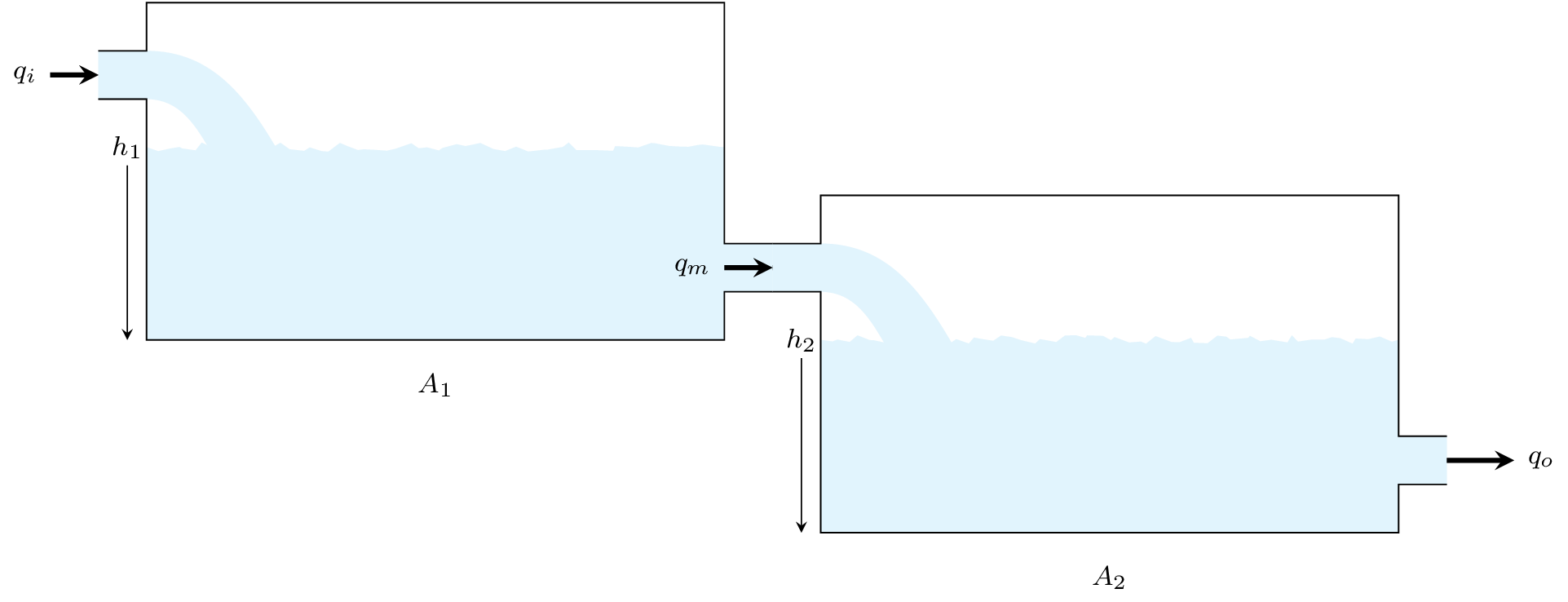
Figura 13 Modelo de dos tanques en cascada.