Método de Po-Shen Loh

Considere una ecuación cuadrática de la forma

\[ x^{2} + bx + c = 0, \]

donde el coeficiente del término cuadrático es 1. Sabemos que las soluciones están dadas por \(x_{1}\) y \(x_{2}\) que pueden ser reales o complejas.

Recordemos que para este tipo de ecuaciones, los coeficientes \(b\) y \(c\) en función de las soluciones están dados como sigue

\[ x_{1} + x_{2} = -b, \]

\[ x_{1} \cdot x_{2} = c. \]

Si obtenemos la gráfica para la ecuación \(x^{2} + 5x + 6\), tenemos

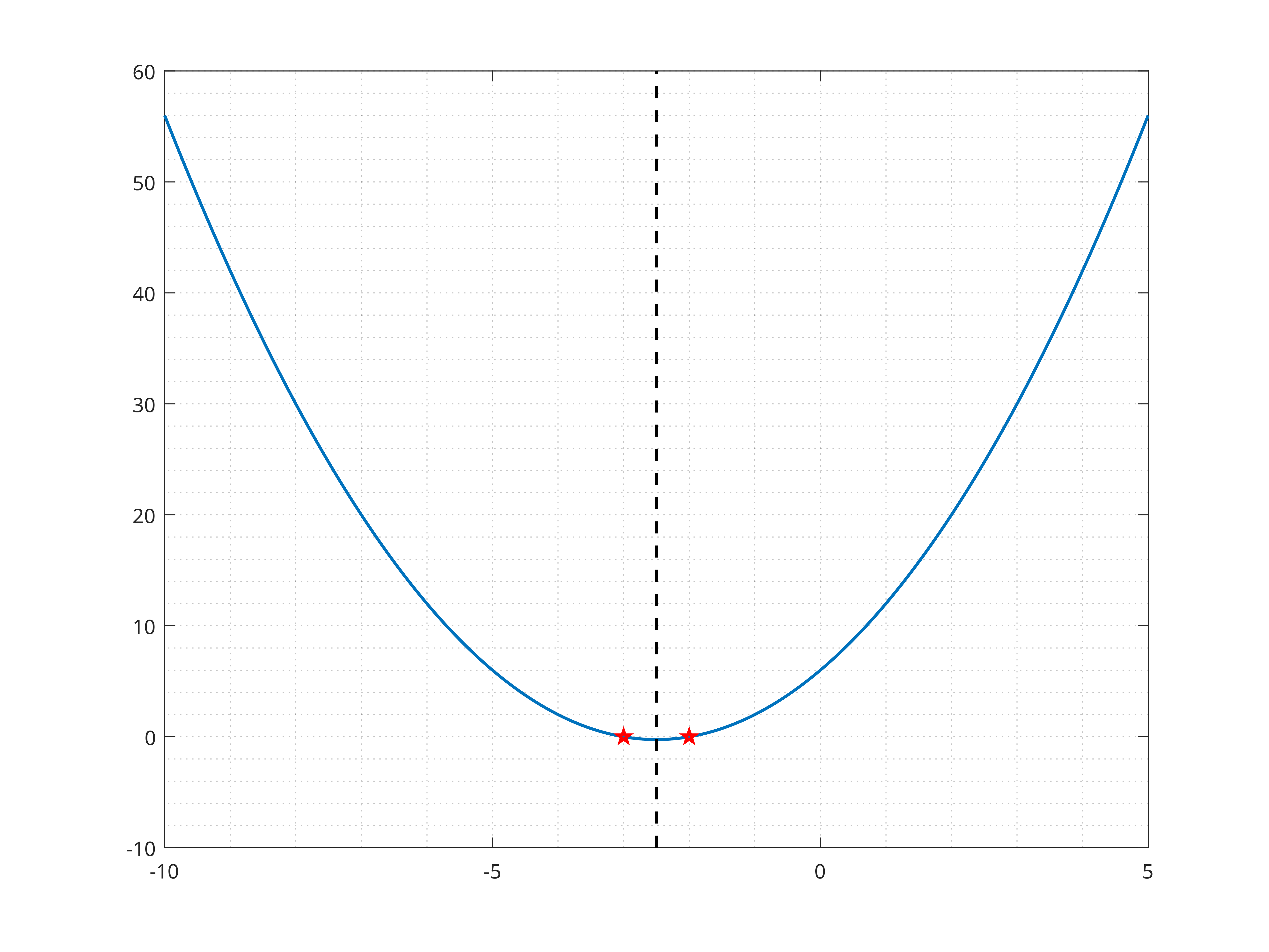
Figura 17 Gráfica de la función \(x^{2} + 5x + 6\) para \(x\in[-10, 5]\) con \(\Delta~t = 1.50\times 10^{-2}\).

donde \(m\) definido como el punto medio entre \(x_{1}\) y \(x_{2}\) está dado como sigue

\[ m = \frac{x_{1}+x_{2}}{2}. \]

La distancia que hay entre \(x_{1}\) y \(m\) la definimos como \(u\) del mismo modo que para \(x_{2}\). Por consiguiente tenemos

\[ x_{1} = m - u, \]

\[ x_{2} = m + u. \]

Tomando en cuenta estas relaciones, se obtiene

\[ m = \frac{x_{1} + x_{2}}{2} = -\frac{b}{2}, \]

\[\begin{split} \begin{aligned} (m - u)(m + u) &= c, \\ m^{2} - u^{2} = c. \end{aligned} \end{split}\]

Despejando \(u\)

\[ u = \sqrt{m^{2} - c} \]

Para el caso de la Figura 17, cuya ecuación cuadrática es \(x^{2} + 5x + 6\), podemos sustituir los valores y tener que

\[ b = 5, \quad c = 6. \]

Por lo tanto

\[ m = \frac{x_{1}+x_{2}}{2} = -2.5, \]

\[ u = \sqrt{m^{2} - c} = \sqrt{(2.5)^{2} - 6} = \sqrt{0.25} = 0.5, \]

Por consiguiente, las raíces son

\[\begin{split} \begin{aligned} x_{1} &= m - u, \\ &= -2.5 - 0.5, \\ &= -3, \end{aligned} \end{split}\]

\[\begin{split} \begin{aligned} x_{2} &= m + u, \\ &= -2.5 + 0.5, \\ &= -2. \end{aligned} \end{split}\]