Modelado de sistemas mecánicos

Movimiento de traslación

Definition 20 (Masa)

Propiedad de un elemento de almacenar energía cinética del movimiento de traslación [Kuo, 1996].

Leyes de Newton

Definition 21 (Primera ley de Newton)

Un objeto permanece en reposo o se sigue moviéndose con velocidad constante en módulo y dirección si ninguna fuerza neta actúa sobre el objeto [Kane et al., 1989].

Definition 22 (Segunda ley de Newton)

La fuerza \(\vec{F}\) necesaria para producir una aceleración \(\vec{a}\) está dada por la siguiente expresión [Kane et al., 1989]

(4)\[ \sum \vec{F} = m\cdot \vec{a} ; \quad \sum F_{x} = m\cdot a_{x}, \quad \sum F_{y} = m\cdot a_{y}, \]

o en término de sus componentes como sigue

(5)\[ \sum F_{x} = m\cdot a_{x}, \quad \sum F_{y} = m\cdot a_{y}, \]

donde \(m\) es la masa del objeto.

Definition 23 (Tercera ley de Newton)

Para toda acción, existe una fuerza de reacción de igual magnitud pero en sentido contrario, donde las fuerzas de acción y reacción actúan sobre objetos diferentes [Kane et al., 1989].

Ley de Hooke

Definition 24 (Ley de Hooke)

La fuerza requerida para estirar o comprimir un resorte \(x\) unidades de longitud a partir de su longitud natural es proporcional a \(x\) como sigue [Thomas et al., 2005]

\[ F = kx, \]

donde \(k\) denota la constante del resorte o constante de fuerza del resorte.

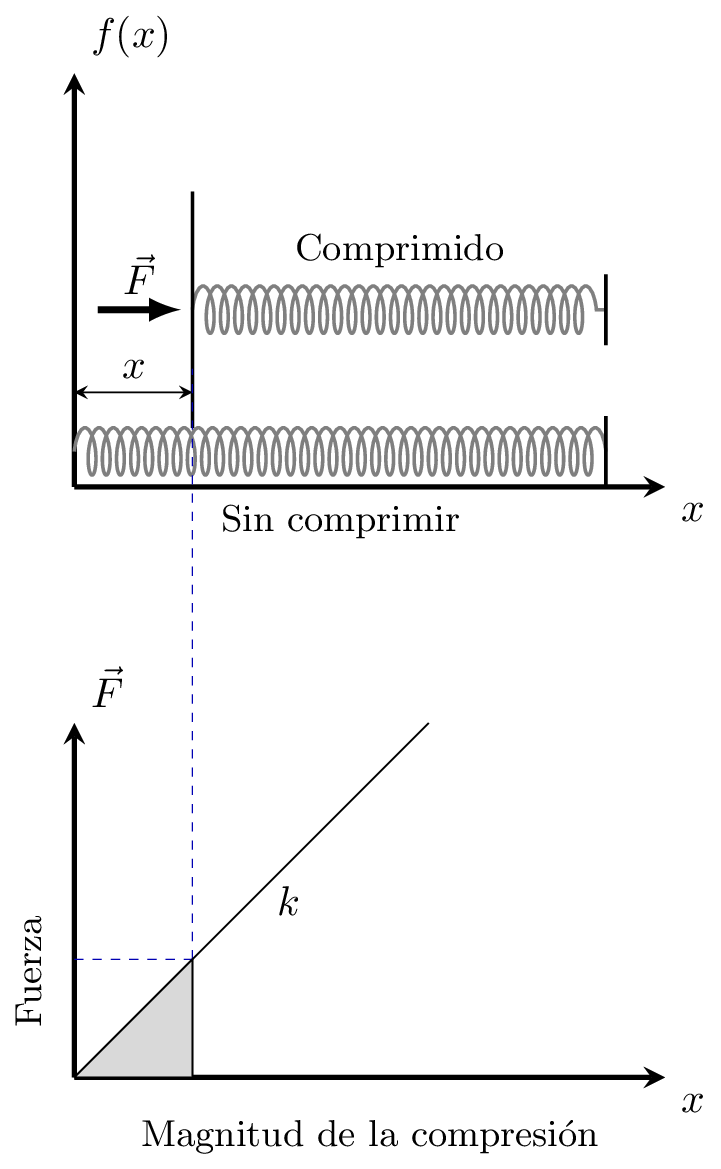
Figura 2 La fuerza \(\vec{F}\) requerida para estirar o comprimir un es proporcional al desplazamiento en \(x\).

Fricción para el movimiento de traslación

Existen tres tipos de fricción que se pueden encontrar en sistemas prácticos: fricción viscosa, fricción estática y fricción de Coulomb las cuales definiremos a continuación.

Definition 25 (Fricción viscosa)

Según Kuo [1996], este tipo de fricción representa una fuerza que es una relación lineal entre la fuerza aplicada y la velocidad.

Suele representarse como un amortiguador como se muestra en la Figura 3 y su expresión matemática está dada como sigue

(6)\[ F_{k} = b \dot{x}, \]

donde \(b\) denota el coeficiente de fricción viscosa.

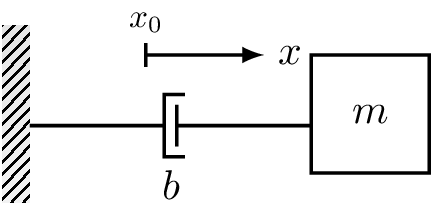
Figura 3 Representación gráfica de un amortiguador para fricción viscosa.

Definition 26 (Fricción estática)

Es una fuerza que previene el movimiento desde el inicio [Kuo, 1996] y está representada por la siguiente ecuación

\[ F_{e} = \left.\pm(F_{s})\right|_{\dot{y}=0}. \]

Este tipo de fricción sólo existe cuando el cuerpo se encuentra estático pero puede moverse. Aquí, el signo de la fricción representa la dirección del movimiento o bien, la dirección inicial de la velocidad.

Definition 27 (Fricción de Coulomb)

Es una fuerza que posee una amplitud constante con respecto al cambio de la velocidad. Sin embargo, el signo de la fuerza de fricción cambia al invertir la dirección de la velocidad [Kuo, 1996]. La relación para este tipo de fricción está dada como sigue

\[ F_{Co} = F_{c} \frac{\dot{x}}{|\dot{x}|}, \]

donde \(F_{c}\) denota el coeficiente de la fricción de Coulomb.

Definition 28 (Movimiento de rotación)

Se define como el movimiento alrededor de un eje fijo. Nos dice que está la suma de los momentos o pares alrededor de un eje fijo es igual al producto de la inercia por la aceleración angular

\[ \sum F = J\cdot \alpha, \]

donde \(J\) denota la inercia, \(a\) la aceleración angular. Otras variables utilizadas para el movimento rotacional son: par (\(\tau\)), velocidad angular (\(\omega\)) y desplazamiento angular (\(\theta\)).

Definition 29 (Inercia)

Propiedad de un elemento de almacenar energía cinética del movimento de rotación. Depende de la composición geométrica al rededor del eje de rotación.

La ecucación que describe el par aplicado a un cuerpo con inercia \(J\), está dada como sigue

\[ \tau(t) = J\cdot \alpha(t) \equiv J \dot{w}(t) \equiv J \ddot{\theta}(t), \]

donde \(\theta(t)\) es el desplazamiento angular, \(\omega(t)\) la velocidad angular y \(\alpha(t)\) la aceleración angular.

Sistema masa-resorte

Considere una masa \(m\) que se desliza sobre una superficie horizontal y que se encuentra sujeta a una superficie vertical a través de un resorte con constante de fuerza \(k\) como se muestra en la Figura 4.

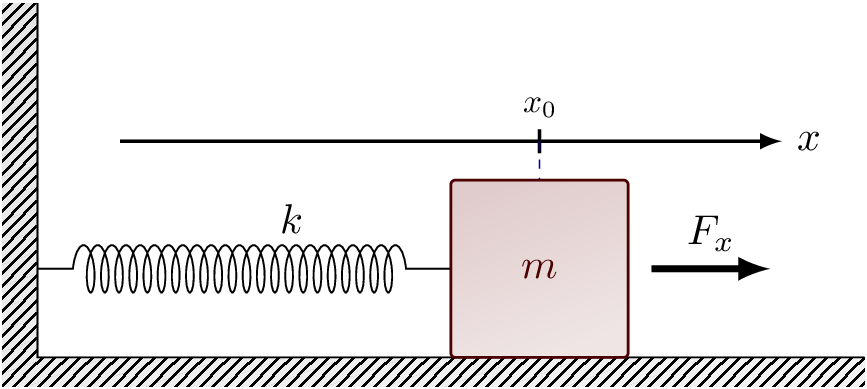
Figura 4 Diagrama del sistema masa-resorte.

Si definimos \(x\) como el desplazamiento desde el punto de referencia \(x_{0}\); asumimos que la masa se desplaza sin fricción y aplicamos la Segunda ley de Newton así como la Ley de Hooke obtenemos

(7)\[ ma + kx = F_{x}. \]

Dado que la aceleración \(a\) está definida como \(\ddot{x}\) y que la fuerza \(F_{x}\) está a nuestra disposición, sustituimos en la ecuación anterior para obtener el modelo del sistema masa-resorte como sigue

\[ m\ddot{x} + kx = 0. \]

Para un desplazamiento largo, la fuerza restauradora (\(kx\)) podría depender de manera no lineal de \(x\), por ejemplo, expresada por la siguiente función

\[ g(x) = k\left( 1 - a^{2}x^{2} \right)x, \quad |ax|<1, \]

representa al modelo llamado softening spring, donde un gran incremento de desplazamiento produce un incremento pequeño de fuerza.

Por otro lado, si tenemos la siguiente función

\[ g(x) = k\left(1 + a^{2}y^{2} \right)x, \]

es posible obtener el modelo llamado hardening spring donde un incremento pequeño de desplazamiento produce un gran incremento de fuerza.

Modelado a partir del enfoque Euler-Lagrange

Cualquier sistema debe satisfacer las ecuaciones de Lagrange dadas por

(8)\[ \frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{\partial \mathcal{L}}{\partial\dot{q}} \right] - \frac{\partial \mathcal{L}}{\partial q} + \frac{\partial J}{\partial \dot{q}} = 0, \]

donde \(\mathcal{L}\) es el Lagrangiano del sistema y se define como sigue

\[ \mathcal{L}(q,\dot{q}) = U^{*}(\dot{q})-T(q). \]

Además

• \(U\), representa la coenergía total en las reservas de flujo del sistema expresada como una función de las coordenadas de esfuerzo generalizado.

• \(T\), la energía total en los almacenes de esfuerzo del sistema expresada como una función de las coordenadas de acumulación de esfuerzo generalizadas.

• \(J\), el co-contenido total en los disipadores del sistema expresado como una función de las coordenadas de esfuerzo generalizado.

• \(q\), el vector de coordenadas generalizadas definida como el conjunto de coordenadas linealmente independientes que definen la configuración del sistema.

Para un sistema mecánico no conservativo, las ecuaciones de Lagrange están dadas como sigue

(9)\[ \frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{\partial \mathcal{L}}{\partial\dot{q}_{j}} \right] - \frac{\partial \mathcal{L}}{\partial q_{j}} + \frac{\partial J}{\partial \dot{q}_{j}} = \tau_{j}, \quad j = 1,\dots,l, \]

donde \(\tau_{j}\) denota las fuerzas generalizadas.

Importante

En este contexto conservativo significa libre de disipación y entradas de fuerzas externas.

Definition 30 (Masa traslacional)

Una masa traslacional pura es un objeto rígido el cual se mueve a través de un entorno no disipativo. De acuerdo con la Segunda ley de Newton, el momento \(p\) de la masa está linealmente relacionado a la velocidad del objeto como se da a continuación

\[ p = mv, \]

donde \(m\) es la masa Newtoniana del objeto. El momento \(p\), está definido por

\[ p = \int_{t_{0}}^{t} F\mathrm{d}t + p(t_{0}), \quad F = \frac{\mathrm{d}p}{\mathrm{d}t}, \]

donde \(F\) denota fuerza.

De acuerdo con la analogía de movilidad, la cantidad de momento es formalmente análoga a la acumulación de flujo. Por lo tanto, una masa pura translacional puede ser clasificada como un almacenamiento de flujo.

La masa Newtoniana, tiene una relación constitutiva lineal intríseca, por consiguiente, la energía almacenada \(U\) (energía cinética) es igual

\[ U = \frac{1}{2}mv^{2}. \]

Definition 31 (Resorte traslacional)

Es un objeto mecánico que cuando está sujeto a una fuerza se comprime o alarga sin aceleración significativa de sus componentes, o pérdida de energía debido a la fricción o falta de la deformación. El mecanismo de almacenamiento de energía de un resorte puro es el desplazamiento neto del resorte desde su estado de reposo. Por lo tanto, la variable desplazamiento se define como

\[ x = \int_{t_{0}}^{t}v\mathrm{d}t + x(t_{0}), \quad v = \frac{\mathrm{d}x}{\mathrm{d}t}. \]

Un resorte lineal ideal obedece la ley de Hooke y tiene una relación constitutiva

\[ x = \frac{1}{k}F, \]

donde \(k\) se conoce como la rigidez del resorte.

De acuerdo con la analogía de movilidad, un resorte es un almacén de esfuerzo, ya que el desplazamiento representa una acumulación de la variable esfuerzo (velocidad). Por lo tanto, la energía almacenada en un resorte es \(T\) (energía potencial) y puede ser evaluada por la siguiente relación constitutiva

\[ T = \frac{1}{2k}F^{2}. \]

Definition 32 (Disipación traslacional)

Un disipador puro es aquel en el que los fenómenos de almacenamiento de energía cinética y potencial están ausentes. Por lo tanto, un objeto rígido y liviano que se mueve a través de un fluido viscoso o se desliza sobre una superficie rugosa tendrá una relación constitutiva que relaciona estáticamente la fuerza aplicada y la velocidad relativa del objeto.

La potencia absorbida por un disipador es el producto de las variables esfuerzo y caudal, y se obtiene de la relación constitutiva como la suma del contenido y cocontenido del disipador. La relación constitutiva de un disipador lineal está dada como sigue

\[ J = G = \frac{1}{2}bv^{2}. \]

En este caso, vamos a tratar de obtener el modelo dinámico del sistema masa-resorte utilizando las ecuaciones de Euler-Lagrange. Para ello, definimos la siguiente coordenada generalizada

\[ q = x, \quad \dot{q} = \dot{x}. \]

Expresamos las energías en función de la coordenada generalizada para obtener el Lagrangiano del sistema. Donde, la energía potencial del sistema se obtiene a partir de la siguiente relación

(10)\[ A = \frac{\text{base}\cdot \text{altura}}{2}, \]

Sustituyendo la Ley de Hooke en (10), tenemos

\[ T = \frac{qkq}{2} \equiv \frac{kq^{2}}{2}, \]

mientras que la co-energía cinética está dada como sigue

\[ U^{*} = \frac{m\dot{q}^{2}}{2}. \]

Por consiguiente, el Lagrangiano del sistema se define como sigue

(11)\[ \mathcal{L}(q,\dot{q}) = \frac{m\dot{q}^{2}}{2} - \frac{kq^{2}}{2}. \]

Calculando las ecuaciones de Lagrange (9) a partir de la Ec. {eq}`eqn:Lagrangiano_mr, obtenemos

\[ \frac{\partial \mathcal{L}}{\partial \dot{q}} = m\dot{q} \]

(12)\[ \frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac{\partial \mathcal{L}}{\partial \dot{q}} \right] = m\ddot{q} \]

(13)\[ \frac{\partial \mathcal{L}}{\partial q} = -kq \]

Finalmente, sustituimos las Ecs. (12) y (13) en la Ec. (9)

\[ m\ddot{x} + kx = F_{x}. \]

Sistema masa-resorte-amortiguador

Considere el sistema masa-resorte-amortiguador mostrado en la Figura 5. Dicho sistema consiste en una masa \(m\) sujeta a un elemento de amortiguamiento con constante de viscosidad \(b\) y un resorte con rigidez \(k\). Podemos observar que el sistema se desplaza sobre un plano horizontal a partir de una fuerza \(F_{x}\) aplicada.

Podemos partir del modelo dado en la Ec. (7) y modelando el amortiguador con la relación dada en la Ec. (6), tenemos

\[ m\ddot{x} + b\dot{x} + kx = F_{x}. \]

De manera análoga, podemos obtener aplicar las ecuaciones de Lagrange {eq}`eqn:sistema_no_conservativo considerando que existe una fuerza de fricción viscosa como sigue

\[ m\ddot{x} + kx = F_{x} - b\dot{x}. \]

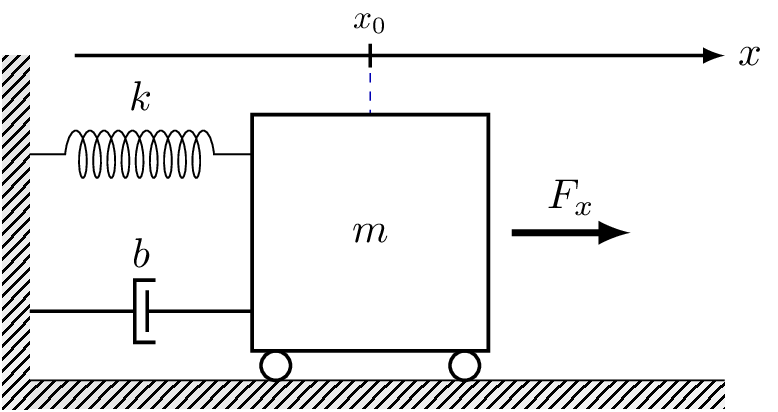
Figura 5 Sistema masa-resorte-amortiguador.

Péndulo simple

Considere el péndulo simple mostrado en la Figura 6

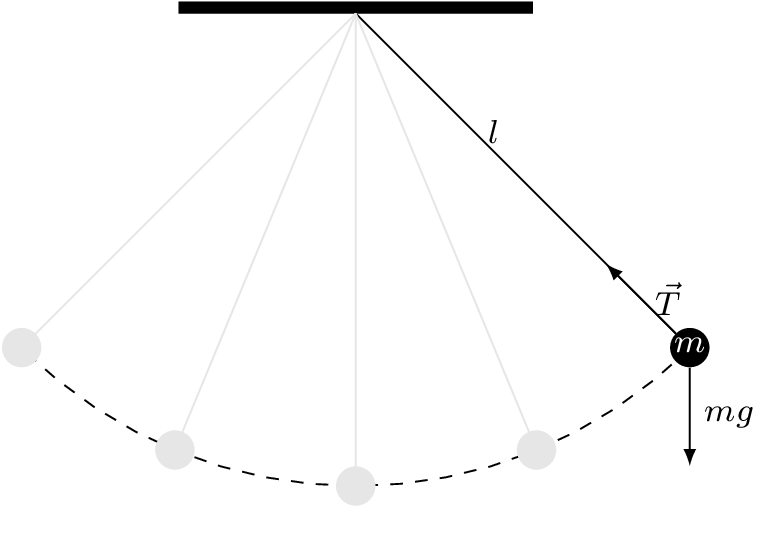
Figura 6 Péndulo simple.

donde \(l\) denota la longitud de la barra, y \(m\) la masa de la bola. Asuma que la barra es rígida y de masa despreciable. Suponga entonces, \(\theta\) como el ángulo entre la barra y el eje vertical a través del pivote. Además, el péndulo se mueve libremente sobre un plano vertical formando un círculo de radio \(l\). Para obtener la ecuación que describe el movimiento del péndulo es necesario identificar las fuerzas que interactúan sobre la bola o bien, utilizar el enfoque de Euler-Lagrange.

Modelado a partir de leyes físicas

En un sistema mecánico de tipo rotacional, las leyes físicas que rigen el sistema están dadas por la Segunda ley de Newton, donde las fuerzas positivas están dadas hacia la derecha mientras que las negativas hacia el lado contrario. Si realizamos un diagrama de cuerpo libre para observar las fuerzas que interactúan con la masa como se muestra a continuación

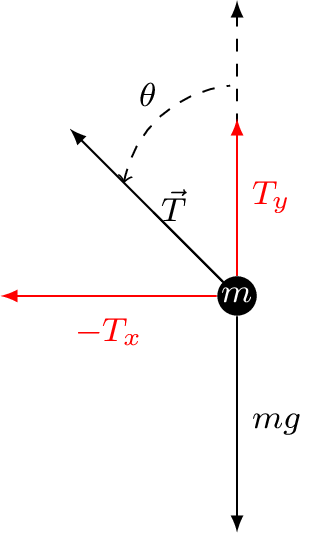
Figura 7 Diagrama de cuerpo libre de la masa en el péndulo simple.

Podemos observar que hay una fuerza gravitacional \(mg\), donde \(g\) es la aceleración de la gravedad. Así mismo, existe una fuerza de tensión \(\vec{T}\) con componentes \(T_{x}\) y \(T_{y}\).

Podemos observar que la única fuerza que interactúa en \(x\) es \(T_{x}\). Recordando que esta tensión tiene una fuerza negativa, por lo tanto la definimos como sigue

(14)\[ -T\sin(\theta) = m \ddot{x}, \]

donde \(T\) denota la magnitud de la tensión y \(\ddot{x}:=\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\).

Para el análisis de las fuerzas que interactúan en el eje \(y\), tenemos

(15)\[ -mg + T\cos(\theta) = m\ddot{y}. \]

Observamos entonces que tenemos dos variables que ecuaciones. Por ello, vamos a relizar el siguiente despeje

(16)\[ T = -\frac{m \ddot{x}}{\sin(\theta)}. \]

Sustituyendo (16) en (15), tenemos

(17)\[ -mg + \left(-\frac{m\ddot{x}}{\sin(\theta)}\right)\cos(\theta) = m \ddot{y}. \]

Simplificamos la expresión obtenida multiplicando ambos lados de la igualdad por el término \(\sin(\theta)\) y resulta

(18)\[ -mg\sin(\theta) - m\ddot{x}\cos(\theta) = m \ddot{y}\sin(\theta). \]

Observando el diagrama de la Figura 6, tenemos que la posición de la masa está dada por sus componentes \(x\) e \(y\) dentro de un plano cartesiano. Así mismo, tenemos que \(l\) y \(\theta\) están en un sistema de coordenadas polares. Por lo tanto, podemos utilizar la relación que hay entre estos sistemas para establecer las siguientes relaciones

(19)\[ x = l\sin(\theta), \quad y = -l\cos(\theta). \]

Puesto que necesitamos la aceleración a lo largo del eje \(x\) e \(y\), derivamos la expresión dada en la Ec. (19) recordando la regla de la cadena (ver Theorem 12)

(20)\[\begin{split} \begin{aligned} \dot{x} &= l\cos(\theta)\dot{\theta}, \\ \dot{y} &= l\sin(\theta)\dot{\theta}, \\ \end{aligned} \end{split}\]

(21)\[\begin{split} \begin{aligned} \ddot{x} &= l \left[\ddot{\theta}\cos(\theta) - \dot{\theta}^{2}\sin(\theta) \right],\\ \ddot{y} &= l \left[\ddot{\theta}\sin(\theta) + \dot{\theta}^{2}\cos(\theta) \right]. \\ \end{aligned} \end{split}\]

Sustituyendo (20) y (21) en (18)

(22)\[\begin{split} \begin{aligned} -mg\sin(\theta) - ml\ddot{\theta}\cos^{2}(\theta) + ml\dot{\theta}^{2}\sin(\theta) \cos(\theta) &= ml \ddot{\theta}\sin^{2}(\theta) + ml\dot{\theta}^{2}\cos(\theta) \sin(\theta), \\ -mg\sin(\theta) - ml\ddot{\theta}\cos^{2}(\theta) &= ml \ddot{\theta}\sin^{2}(\theta), \\ -mg\sin(\theta) &= ml\ddot{\theta} \left[\sin^{2}(\theta) + \cos^{2}(\theta)\right], \\ \end{aligned} \end{split}\]

(23)\[ ml\ddot{\theta} = -mg\sin(\theta). \]

Suponiendo que hay una fuerza proporcional a la velocidad de la masa con un coeficiente \(k_{f}\) que resiste el movimiento, el modelo de péndulo simple con fuerza de fricción} queda dado por la siguiente ecuación

(24)\[ ml\ddot{\theta} = -mg\sin(\theta) - k_{f}l\dot{\theta}. \]

Por lo tanto, la dinámica del péndulo simple con y sin fricción están dadas por ecuaciones diferenciales de segundo orden. Para resolver las Ec. (23) y (24) realizamos un cambio de variable y definimos como variables de estado \(x_{1} = \theta\) y \(x_{1} = \dot{\theta}\). Por consiguiente, el sistema queda representado como sigue

(25)\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= -\frac{g}{l} \sin(x_{1}) - \frac{k_{f}}{m}x_{2}. \end{aligned} \end{split}\]

Una variante del sistema de péndulo simple se puede obtener agregando una entrada exógena \(\tau\)

\[\begin{split} \begin{aligned} \dot{x}_{1} &= x_{2}, \\ \dot{x}_{2} &= -\frac{g}{l} \sin(x_{1}) - \frac{k_{f}}{m}x_{2} + \frac{\tau}{ml^{2}}. \end{aligned} \end{split}\]

Modelado a partir del enfoque Euler-Lagrange

El sistema mostrado en la Figura 6, sólo posee un grado de libertad denotado como \(\theta\). Entonces, definimos las siguientes coordenadas generalizadas

\[ q := \theta, \quad \dot{q} := \dot{\theta}. \]

Además, definimos como fuerza generalizada la variable \(u\), i.e.

\[ \tau_{i} = 0. \]

Ahora bien, podemos representar la Ec. (19) en forma vectorial como sigue

(26)\[\begin{split} p_{m} = \begin{bmatrix} x_{m} \\ y_{m} \end{bmatrix} = \begin{bmatrix} l\sin(\theta) \\ -l\cos(\theta) \end{bmatrix}, \end{split}\]

y el vector de velocidad (20) como sigue

(27)\[\begin{split} v_{m} = \begin{bmatrix} \dot{x}_{m} \\ \dot{y}_{m} \\ \end{bmatrix} = \begin{bmatrix} l\cos(\theta)\dot{\theta} \\ l\sin(\theta)\dot{\theta} \\ \end{bmatrix}. \end{split}\]

La energía co-cinética del sistema está dada por

(28)\[\begin{split} \begin{aligned} U^{*} = \frac{1}{2}mv^{2} &\equiv \frac{1}{2}m\|v_{m}\|^{2}\\ &= \frac{1}{2}mv_{m}^{T}v_{m}. \end{aligned} \end{split}\]

mientras que la energía potencial del sistema por

(29)\[ T = mgh \equiv m\vec{g}^{T}p_{m}, \]

donde \(\vec{g} = \begin{bmatrix} 0 & g \end{bmatrix}^{T}\), con \(g \in \mathbb{R}^{2}\).

Sustituyendo (27) en (28), tenemos

\[\begin{split} \begin{aligned} U^{*} &= \frac{1}{2}m \begin{bmatrix} l\cos(\theta)\dot{\theta} & l\sin(\theta)\dot{\theta} \end{bmatrix} \begin{bmatrix} l\cos(\theta)\dot{\theta} \\ l\sin(\theta)\dot{\theta} \\ \end{bmatrix} \\ &= \frac{1}{2}m \left( l^{2}\cos^{2}(\theta)\dot{\theta}^{2} + l^{2}\sin^{2}(\theta)\dot{\theta}^{2} \right), \\ &= \frac{1}{2} ml^{2}\dot{\theta}^{2} \left( \cos^{2}(\theta) + \sin^{2}(\theta) \right), \\ &= \frac{1}{2} ml^{2}\dot{\theta}^{2}. \end{aligned} \end{split}\]

Ahora, sustituyendo (26) en (29)

\[\begin{split} \begin{aligned} T &= m \begin{bmatrix} 0 & g \end{bmatrix} \begin{bmatrix} l\sin(\theta) \\ -l\cos(\theta) \end{bmatrix}, \\ &= -mgl\cos(\theta) \end{aligned} \end{split}\]

Entonces, el Lagrangiano del sistema se define como sigue

\[ \mathcal{L} = \frac{1}{2}ml^{2}\dot{\theta}^{2} + mgl\cos(\theta). \]

Obtenemos las derivadas parciales

(30)\[ \frac{\partial \mathcal{L}}{\partial \dot{\theta}} = ml^{2}\dot{\theta}, \]

(31)\[ \frac{\mathrm{d}}{\mathrm{d}t}\left[ \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \right]= ml^{2}\ddot{\theta}, \]

(32)\[\begin{split} \begin{aligned} \frac{\partial \mathcal{L}}{\partial \theta} &= \frac{\partial}{\partial \theta} \left( \frac{1}{2}ml^{2}\dot{\theta}^{2} + mgl\cos(\theta) \right), \\ &= -mgl\sin(\theta), \end{aligned} \end{split}\]

Sustituyendo, (30)-(32) en (9) y considerando que \(\tau=0\) tenemos

\[ ml^{2}\ddot{\theta} + mgl\sin(\theta) = 0. \]